Tóm tắt về RNN & LSTM
Thực ra, các bài toán về Nartual Language Processing(NLP) không phải là thế mạnh của mình. Từ trước đến giờ, mình chủ yếu làm các bài toán về Computer Vision(CV). Tuy nhiên, trong thời gian gần đây, cộng đồng nói rất nhiều về Attention, Transformer, BERT, …. Đó là những kỹ thuật tiên tiến mới ra đời, giúp giải quyết rất nhiều tác vụ khó của NLP, đạt đến độ State of Art. Hoạt động trong lĩnh vực AI đã lâu, mình không muốn đứng ngoài dòng chảy công nghệ đó. Mặc dù bên CV, mình còn rất nhiều thứ muốn viết, nhưng trong một số bài viết sắp tới mình muốn “đổi gió” một chút. Mình sẽ viết về các kỹ thuật sử dụng trong NLP, sau khi đã dành ra kha khá thời gian để tìm hiểu về chúng. Mục đích viết vẫn là để ghi nhớ và chia sẻ với mọi người. Các kỹ thuật mình dự định viết sẽ bao gồm: RNN, LSTM, Transformer, BERT, Attention, Seq2Se2, …
Bài đầu tiên trong chủ đề NLP, mình sẽ cùng các bạn tìm hiểu về RNN.
Nếu như các bên CV có CNN thì bên NLP có RNN. CNN chuyên xử lý dữ liệu có kiến trúc dạng lưới (grid), (VD: Images, …), còn RNN chuyên xử lý dữ liệu dạng chuỗi (sequential).
1. Overview
1.1 Kiến trúc RNN
Giả sử:
- $X_t \in R^{n\times d}$ là Input tại Time-Step $t$,
- $h_t \in R^{n\times h}$ là Hidden State tại Time-Step $t$,
- $W_{xh} \in R^{d\times h}$ là ma trận trọng số của Hidden State tại Time-Step $t$,
- $b_h \in R^{1\times h}$ là hệ số Bias của Hidden State tại Time-Step $t$,
- $h_{t-1}$ là Hidden State tại Time-Step $t-1$,
- $W_{hh} \in R^{h\times h}$ là ma trận trọng số của Hidden State tại Time-Step $t-1$,
- $W_{hq} \in R^{h\times q}$ là ma trận trọng số của Output Layer tại Time-Step $t$
- $b_q \in R^{1\times h}$ là hệ số Bias của Output Layer tại Time-Step $t$,
- $\phi$ là hàm kích hoạt.

Khi đó:
-
Trạng thái của Hidden Layer tại Time_Step $t$ sẽ là:
$h_t = \phi(X_tW_{xh} + h_{t-1}W_{hh} + b_h)$
-
Giá trị đầu ra tại Time-Step $t$ sẽ là:
$O_t = h_tW_{hq} + b_q$
1.2 Ưu điểm, nhược điểm của RNN
Ưu điểm:
- Có khả năng xử lý dữ liệu đầu vào ở bất kỳ độ dài nào.
- Kích thước mô hình không tăng theo kích thước đầu vào.
- Việc huấn luyện mô hình có sử dụng thông tin ở Time-Step trước đó.
- Các hệ số của mô hình (weight và bias) được chia sẻ theo thời gian.
Nhược điểm:
- Việc xử lý, tính toán mất khá nhiều thời gian.
- Thông tin từ các Time-Step ở xa không được duy trì tốt.
- Không thể xem xét bất kỳ đầu vào nào trong tương lai cho trạng thái hiện tại.
1.3 Một số loại mô hình RNN
-
Dạng 1: One-to-One

-
Dạng 2: One-to-Many
Ứng dụng: Music generation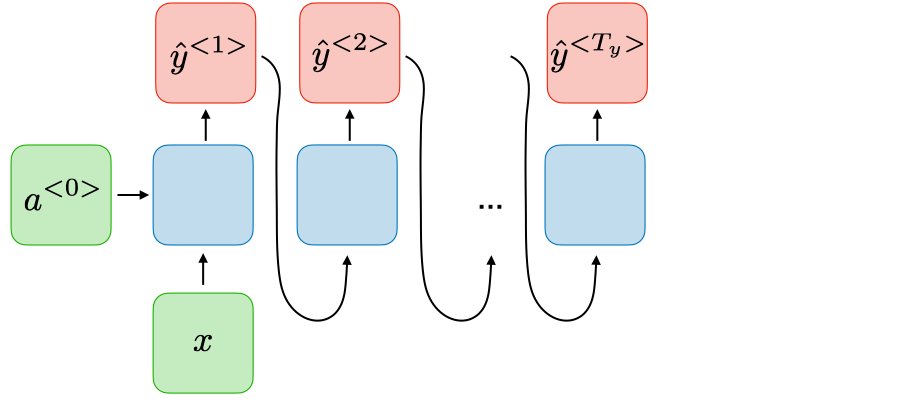
-
Dạng 3: Many-to_One
Ứng dụng: Sentiment classification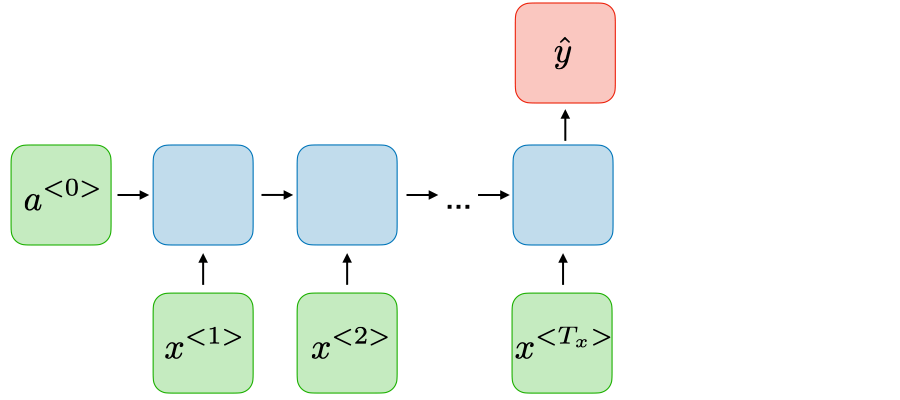
-
Dạng 4: Many-to-Many (Input Data và Ouput có chiều dài bằng nhau)
Ứng dụng: Name entity recognition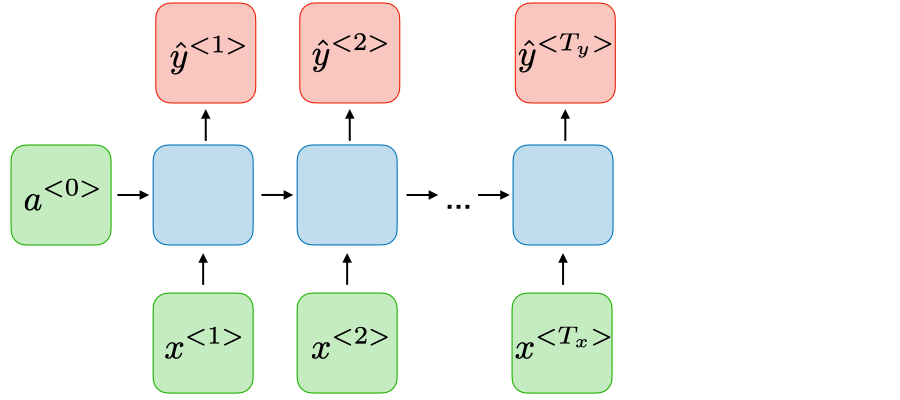
-
Dạng 4: Many-to-Many (Input Data và Ouput có chiều dài khác nhau)
Ứng dụng: Machine translation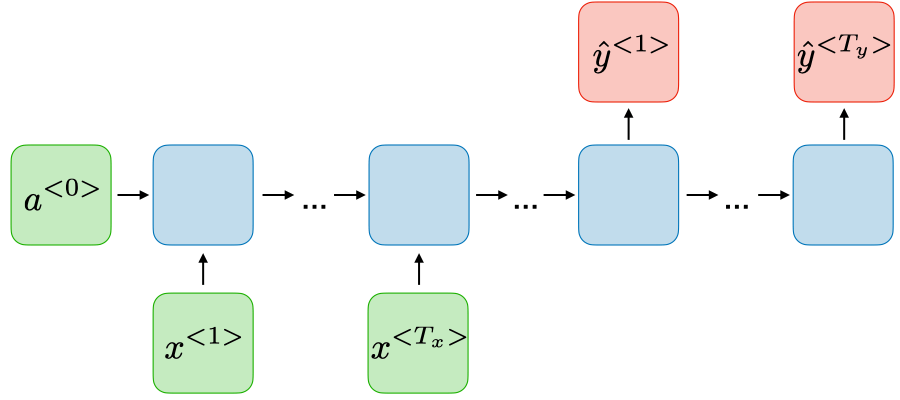
1.4 Loss Function
Loss Function của RNN bằng tổng các Loss tại các Time-Step:
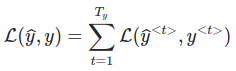
1.5 Backpropagation through time
Backpropagation được thực hiện tại mỗi Time-Step. Tại Time-Step T, đạo hàm của Loss Function $L$ đối với ma trận trọng số $W$ được cho bởi công thức:
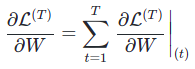
2. Xử lý vấn đề Long Term Dependences
Bình thường thì RNN sử dụng 1 trong 3 Activation Function là: Sigmoid, Tanh và ReLU.
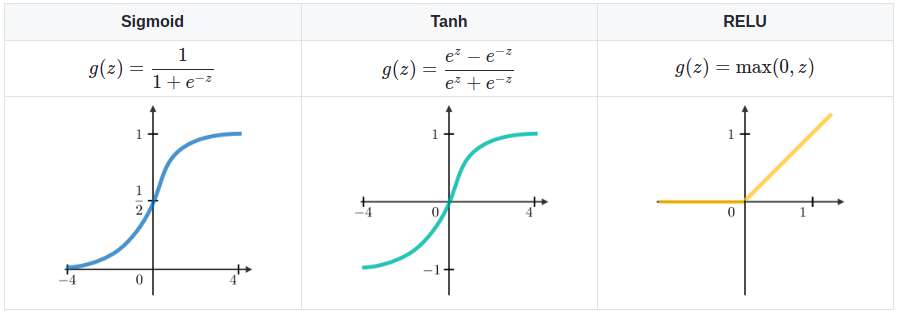
Cũng giống như các mô hình khác, hiện tượng Vanishing & Exploring Gradient cũng xảy ra ở trong mô hình RNN. Điều này dẫn đến việc RNN không có khả năng ghi nhớ trạng thái của các Time-Step ở xa. Nguyên nhân của các hiện tượng này là do việc thực hiện phép nhân Gradient theo hàm mũ, làm cho nó tăng/giảm một các đột biến khi số lượng Layers tăng lên.
Sử dụng ReLU chúng ta đã giải quyết được khá tốt vấn đề Vanishing Gradient. Còn đối với Exploring Gradient, chúng ta có thể sử dụng Gradient Clipping.
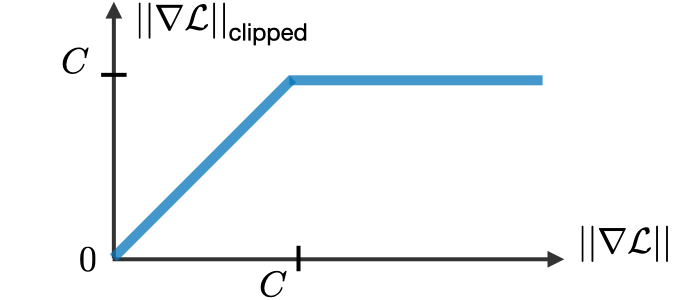
Ý tưởng của Gradient Clipping cũng tương tự như ReLU, nó đưa ra một giới hạn, và Gradient chỉ có thể nhỏ hơn hoặc bằng giới hạn đó.
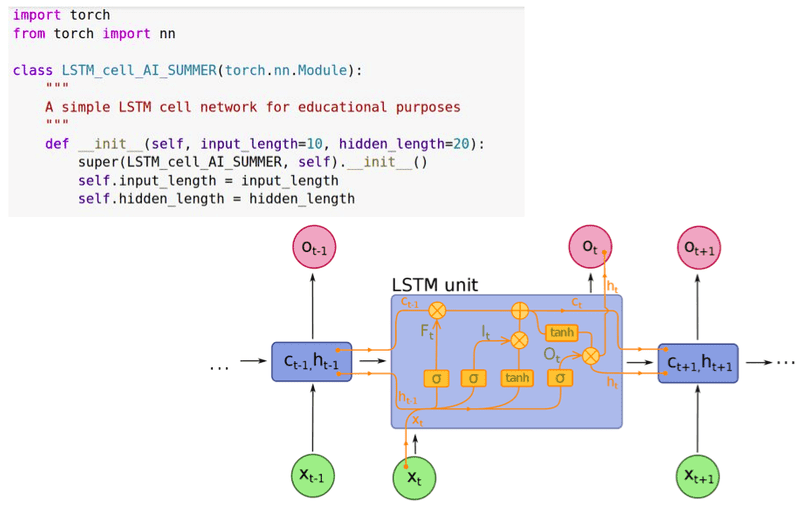
3. Long Short Team Memory (LSTM)
Long Short Team Memory (LSTM)) là một phiên bản cải tiến của RNN, giúp dễ dàng ghi nhớ dữ liệu quá khứ trong bộ nhớ của nó. Vấn đề Vanishing Gradient của RNN được giải quyết tốt hơn với LSTM. LSTM rất phù hợp giải quyết các bài toán phân loại, xử lý và dự đoán chuỗi thời gian có độ dài không xác định. Mô hình LSTM cũng được huấn luyện bằng cách thuật toán Backpropagation.
Kiến trúc mạng LSTM bao gồm nhiều Layers, mỗi Layers được cấu tạo bởi nhiều đơn vị nhỏ gọi là Cell. Mỗi Cell được đại diện bởi 2 bộ nhớ: Cell State ($C$) và Hidden State ($h$).
- Hidden State - h,H: Bộ nhớ ngắn hạn (working memory), chỉ lưu thông tin của Cell ngay trước Cell hiện tại. Tồn tại trong cả RNN và LSTM. Hidden State cũng chính là Ouput của RNN/LSTM Cell.
- Cell State - C: Bộ nhớ dài hạn (long-term memory, memory cell), lưu thông tin của nhiều Cells trong quá khứ. Chỉ tồn tại trên LSTM.
Xét 1 Cell hiện tại ($C_t, h_t$) trong LSTM. Luồng dữ liệu trong Cell này tuần tự đi qua 3 cổng như sau:
- Forget gate: Cổng này quyết định thông tin nào từ Cell trước đó ($C_{t-1}$) nên được giữ lại hoặc ném đi. Thông tin từ Hidden State trước đó ($h_{t-1}$) và thông tin từ Input hiện tại ($x_t$) được đưa qua hàm Sigmoid, cho ra một giá trị trong khoảng từ 0 đến 1. Giá trị này càng gần 0 nghĩa là thông tin ít quan trọng (*trường hợp = 0 thì có thể bỏ qua - Forget*), giá trị càng gần 1 nghĩa là thông càng tin quan trọng.
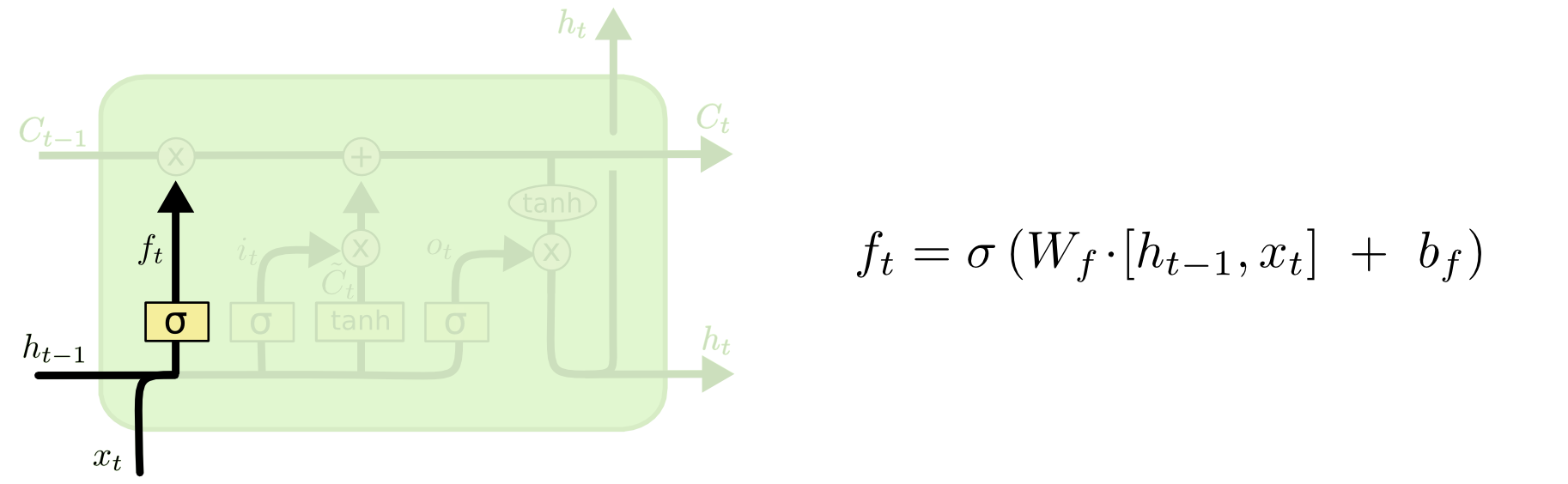
$f_t = \sigma(W_f\cdot[h_{t-1},x_t] + b_f) = \sigma(W_{xf}X_t + W_{hf}h_{t-1} + b_f)$
- Input gate: Cổng này quyết định giá trị nào từ Hidden State trước đó ($h_{t-1}$) và thông tin từ Input hiện tại ($x_t$) sẽ được đi vào Cell hiện tại. Để làm được việc này, nó sử dụng 2 hàm Sigmoid và Tanh. Tương tự như Forget Gate, thông tin từ Hidden State trước đó ($h_{t-1}$) và thông tin từ Input hiện tại ($x_t$) được đưa qua hàm Sigmoid, cho ra một giá trị trong khoảng từ 0 đến 1. Giá trị này càng gần 0 nghĩa là thông tin càng ít quan trọng , giá trị càng gần 1 nghĩa là thông tin càng quan trọng. Hàm Tanh tạo ra một vector ứng cử của Cell State hiện tại ($\widetilde{C_t}$). Output của 2 hàm này được nhân với nhau tính toán Cell State hiện tại.
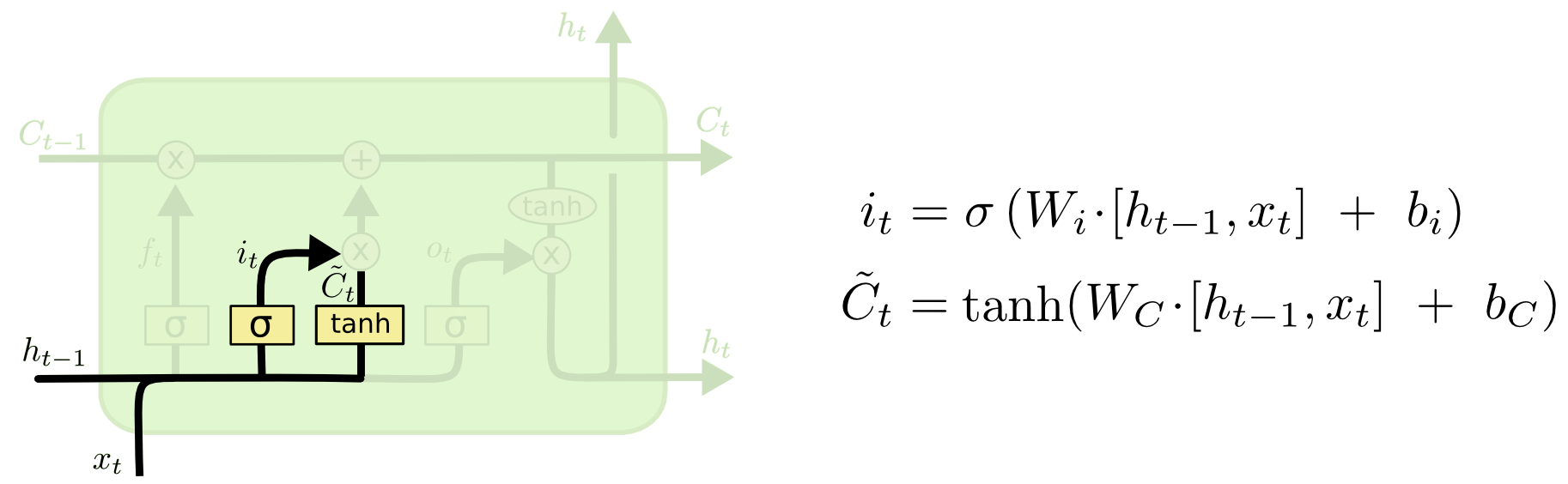
$i_t = \sigma(W_i\cdot[h_{t-1},x_t] + b_i) = \sigma(W_{xi}X_t + W_{hi}h_{t-1} + b_i)$
$\widetilde{C_t} = tanh(W_c\cdot[h_{t-1},x_t] + b_c) = tanh(X_tW_{xc} + h_{t-1}W_{hc} + b_c)$
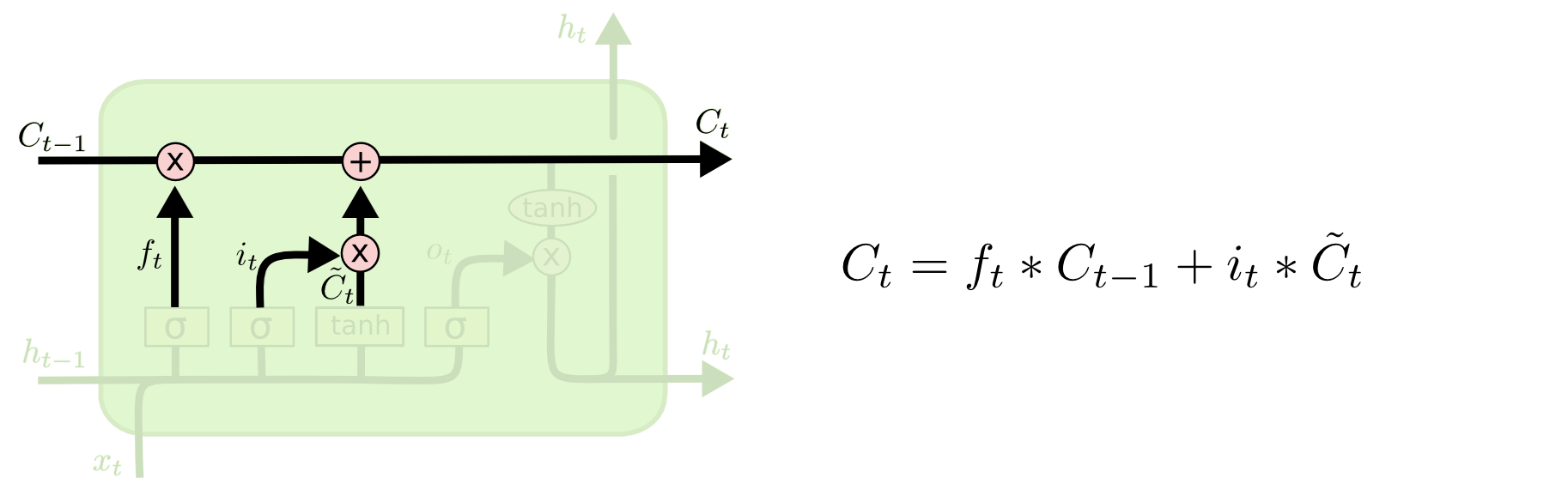
Đến đây, ta đã có thể tính được Cell State hiện tại:
Chú giả về các phép toán:
$\otimes$: Element-wise multiplication
$\oplus$: Element-wise addition
Chúng ta nhân trạng thái của Cell trước đó với $f_t$ rồi cộng với $i_t * \widetilde{C_t}$
$C_t = f_t * C_{t-1} + i_t * \widetilde{C_t}$
- Output gate: Cổng này quyết định thông tin nào sẽ được output ra ngoài ($h_t$). Vẫn vẫn giống như 2 cổng bên trên, thông tin từ Hidden State trước đó ($h_{t-1}$) và thông tin từ Input hiện tại ($x_t$) được đưa qua hàm Sigmoid, cho ra một giá trị trong khoảng từ 0 đến 1. Giá trị này càng gần 0 nghĩa là thông tin càng ít quan trọng , giá trị càng gần 1 nghĩa là thông tin càng quan trọng. Tiếp đó, Cell State được cho qua hàm Tanh để đưa giá trị của Cell State về miền [-1,1].
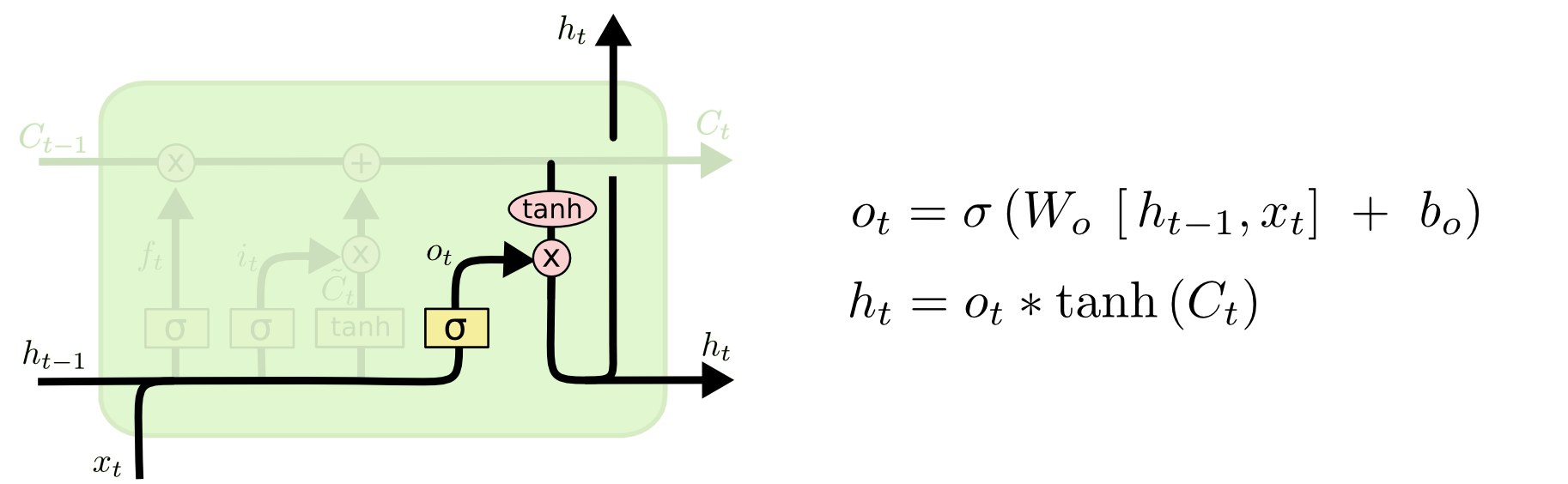
Output của Cell được tính như sau:
$o_t = \sigma(W_o\cdot[h_{t-1},x_t] + b_o) = \sigma(W_{xo}X_t + W_{ho}h_{t-1} + b_o)$
$h_t = o_t * tanh(C_t)$
4. Kết luận
Trong bài này, chúng ta đã tóm tắt sơ lược về RNN & LSTM. Mặc dù LSTM tiên tiến hơn RNN nhưng nó vẫn còn tồn tại một số nhược điểm.
Trong bài tiếp theo, chúng ta sẽ cùng tìm hiểu về cơ chế Attention và kiến trúc Transformer. Mời các bạn đón đọc.
5. Tham khảo