Tìm hiểu Siamese Neural Network
Ngày nay, AI đã len lỏi vào mọi lĩnh vực của đời sống xã hội: y tế, giáo dục, giao thông, … Có thể nói không ngoa rằng hầu như mọi bài toán AI đều có thể giải quyết được thông qua Neural Network (NN). Tuy nhiên, các NNs luôn đòi hỏi lượng lớn dữ liệu để huấn luyện chúng. Trong thực tế, có một số bài toán mà việc thu thập đủ dữ liệu là một nhiệm vụ bất khả thi, ví dụ như bài toán Face Recognition, Signature Verification, … Siamese Network (SN) hay Siamese Neural Network (SNN) ra đời để giải quyết tốt hơn những bài toán dạng như thế này.
SNN chỉ sử dụng một số lượng hình ảnh rất nhỏ (vài ảnh) để có được những dự đoán tốt hơn nhiều so với mạng NN truyền thống. Vì thế nó còn được gọi với 1 số cái tên như One-shot Learning, Few-shot Learning, … Khả năng học hỏi từ rất ít dữ liệu đã khiến cho SNN trở nên phổ biến hơn trong những năm gần đây. Trong bài viết này, chúng ta sẽ tìm hiểu nó là gì và cách phát triển hệ thống Signature Verification với Pytorch bằng cách sử dụng SNN.
1. Giới thiệu Siamese Neural Network
Siamese Neural Network (SNN) là một kiến trúc mạng nơ-ron chứa hai hoặc nhiều mạng con giống hệt nhau. “Giống hệt nhau” ở đây có nghĩa là, chúng có cùng cấu hình với cùng thông số và trọng số. Việc cập nhật các thông số được phản ánh đồng thời trên cả hai mạng con của nó.
SNN được sử dụng để tìm sự giống nhau của các dữ liệu đầu (Input Data) vào bằng cách so sánh các vectơ đặc trưng của chúng. Một số ứng dụng phổ biến của SNN có thể kể đến như là: Face Verification, Signature Verification, Image Seaching System, …
Thông thường, một mạng nơ-ron học cách để dự đoán các lớp của một bài toán. Nếu muốn thêm hay bớt các lớp mới, chúng ta phải cập nhật (huấn luyện) lại mạng nơ-ron trên toàn bộ tập dữ liệu (cả dữ liệu mới và cũ). Ngoài ra, các mạng nơ-ron sâu cần một khối lượng lớn dữ liệu để có thể huấn luyện chúng. SNN, theo một cách khác, học cách tìm ra sự giống nhau giữa các Input Data. Vì vậy, nó cho phép chúng ta phân loại các lớp dữ liệu mới mà không cần huấn luyện lại mạng nơ-ron.
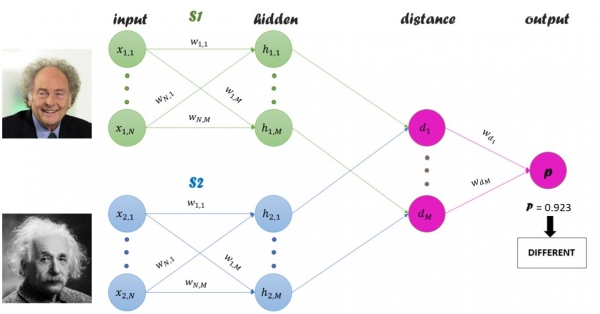
Luồng làm việc của SNN như sau:
- Chọn một cặp Input Data (trong phạm vi bài này là ảnh) được chọn từ dataset.
- Đưa mỗi ảnh qua mỗi Sub-network của SNN để xử lý. Output của các Sub-networks là một Embedding vector.
- Tính toán khoảng cách Euclidean giữa 2 Embedding vectors đó.
- Một Sigmoid Function có thể được áp trên khoảng cách để đưa ra giá trị Score trong đoạn [0,1], thể hiện mức độ giống nhau giữa 2 Embedding vectors. Score càng gần 1 thì 2 vectors càng giống nhau và ngược lại.

2. Ưu điểm của SNN
SNN có một số ưu điểm nổi bật như sau:
-
Lượng dữ liệu cần thiết để huấn luyện SNN là rất ít. Chỉ cần vài Samples là đủ (1-5 samples) huấn luyện SNN. Phương pháp mà nó sử dụng ở đây là One-Shot Learning hoặc Few-Shot Learning. Chính vì cần ít dữ liệu huấn luyện như vậy nên chúng ta cũng không lo lắng việc dữ liệu bị mất cân bằng (Image Imbalance).
-
Khả năng kết hợp với các bộ phân loại khác cao. Do cơ chế học của SNN khác biệt với các bộ phân lớp thông thường khác, nên chúng ta hoàn toàn có thể kết hợp chúng lại với nhau. Việc làm này thường cho ra kết quả tốt hơn.
-
Học từ sự tương đồng về ngữ nghĩa: SNN tập trung vào việc học các Features ở các lớp sâu hơn, nơi mà các Features giống nhau được đặt gần nhau. Do đó, nó có thể hiểu được phần nào sự tương đồng về ngữ nghĩa của các Input Data.
3. Nhược điểm của SNN
SNN cũng có những nhược điểm sau:
-
Thời gian huấn luyện lâu hơn. SNN học theo từng cặp đôi một với nhau nên khả năng học của nó chậm hơn các NN khác.
-
Không thể hiện xác suất mỗi lớp trong Output. SNN chỉ đưa đưa 1 giá trị Score trong đoạn [0,1], thể hiện sự giống nhau giữa 2 Input Data. Score càng gần 1 thì 2 Input Data càng giống nhau và ngược lại.
4. Loss Function của SNN
Bởi vì, SNN học theo kiểu từng đôi một của Input Data nên Cross Entropy Loss Function thường không được sử dụng. Thay vào đó, 2 Loss Functions là Triple Loss và Contrastive Loss được sử dụng nhiều hơn.
4.1 Triple Loss function
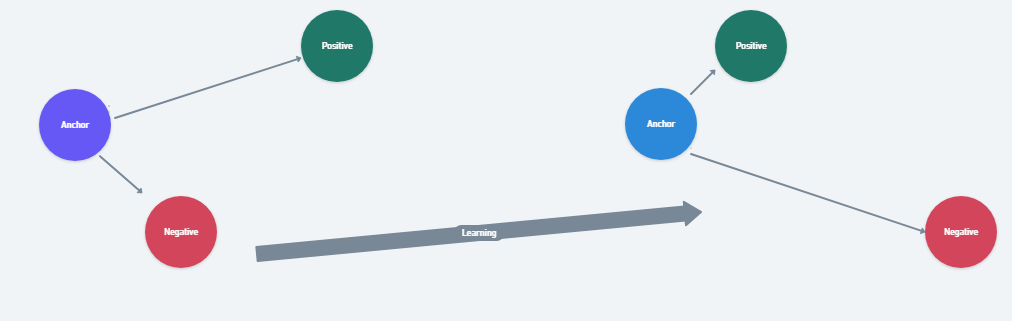
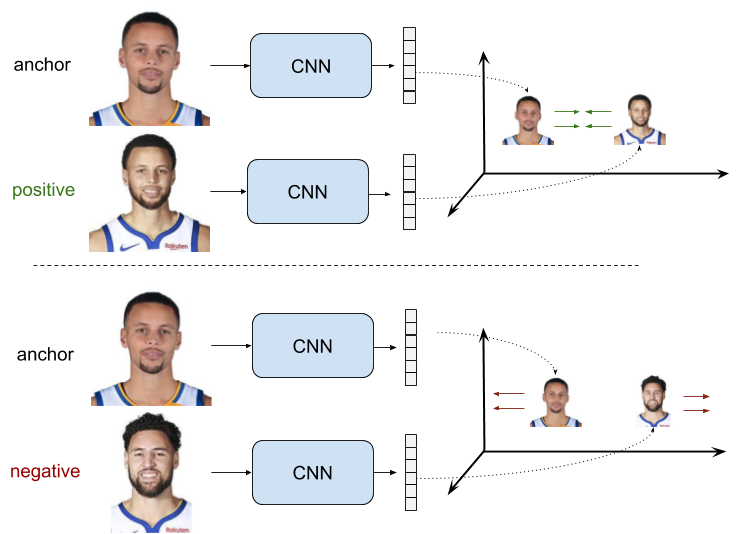
Ý tưởng của Triple Loss là sử dụng bộ 3 Input Data bao gồm: Anchor (A), Positive (P) và Nagative (N) mà ở đó, khoảng cách từ A đến P được tối thiểu hóa, trong khi khoảng cách từ A đến N được tối đa hóa trong suốt quá trình huấn luyện model.
$L(A,P,N) = max(||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + \alpha,0)$
Trong công thức trên,
- $\alpha$ gọi là margin, được sử dụng để nhấn mạnh sự khác biệt hoặc sự tương đồng giữa các cặp Input Data.
- $f(A), f(P), f(N)$ là các vectors đặc trưng của các Input Data A, P, N, tương ứng.
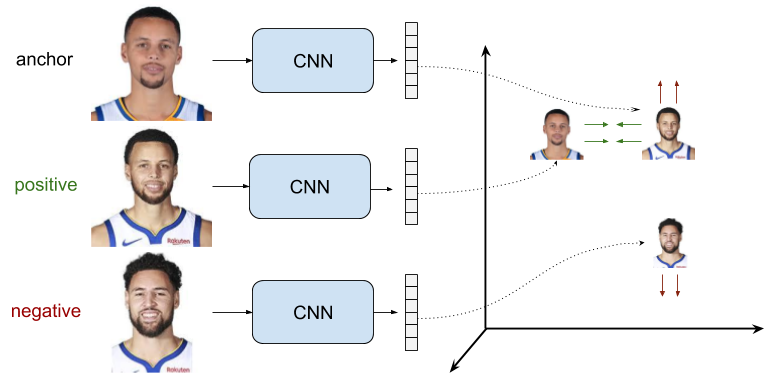
4.2 Contrastive Loss
Ý tưởng của Contrastive Loss cũng tương tự như Triplet Loss, sự khác nhau ở chỗ Contrastive Loss chỉ sử dụng 1 cặp Input Data, hoặc là cùng loại, hoặc là khác loại. Nếu cùng loại thì khoảng cách giữa các vectors đặc trưng của chúng sẽ được tối thiểu hóa, còn nếu khác loại thì khoảng cách giữa các vectors đặc trưng của chúng sẽ được tối đa hóa trong suốt quá trình huấn luyện.
Công thức của Contrastive Loss:
$(1 - Y)\frac{1}{2}(D_w)^2 + (Y)\frac{1}{2}{max(0,m - D_w)}^2$
Trong đó, $D_w$ là khoảng cách Euclidean:
$\sqrt{{G_w(X_1) - G_w(X_2)}^2}$
$G_w$ là Ouput của SNN đối với 1 Input Data.
Việc lựa chọn sử dụng Loss Function nào còn tùy thuộc vào bài toán cụ thể. Chưa có công bố nào kết luận cái nào tốt hơn cái nào. Bạn nên thử cả 2 loại để tìm ra cái tốt hơn cho bài toán của bạn.
5. Signature Verification với Siamese Networks
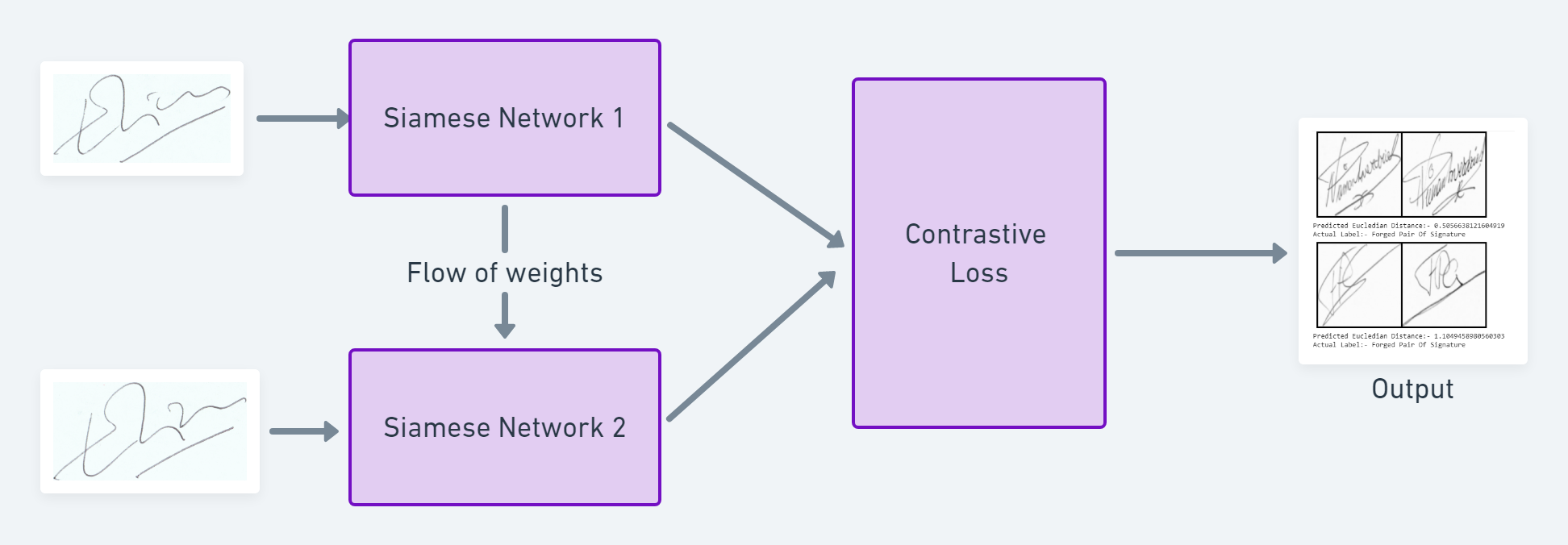
Trong phần này, chúng ta sẽ xây dựng một SNN model bằng Pytorch để thực hiện nhiệm vụ Signature Verification.
5.1 Signature dataset
Dataset sử dụng trong bài này là ICDAR 2011. Nó chứa các chữ ký của những người dân ở Hà Lan, cả chữ ký thật và chữ ký giả. Nhãn của dữ liệu nằm trong file CSV tương ứng.

Chúng ta sẽ đoc vào dataset và chuẩn bị cho việc huấn luyện model:
#preprocessing and loading the dataset
class SiameseDataset():
def __init__(self,training_csv=None,training_dir=None,transform=None):
# used to prepare the labels and images path
self.train_df=pd.read_csv(training_csv)
self.train_df.columns =["image1","image2","label"]
self.train_dir = training_dir
self.transform = transform
def __getitem__(self,index):
# getting the image path
image1_path=os.path.join(self.train_dir,self.train_df.iat[index,0])
image2_path=os.path.join(self.train_dir,self.train_df.iat[index,1])
# Loading the image
img1 = Image.open(image1_path)
img2 = Image.open(image2_path)
img1 = img0.convert("L")
img2 = img1.convert("L")
# Apply image transformations
if self.transform is not None:
img1 = self.transform(img1)
img2 = self.transform(img2)
return img1, img2 , th.from_numpy(np.array([int(self.train_df.iat[index,2])],dtype=np.float32))
def __len__(self):
return len(self.train_df)
# Load the the dataset from raw image folders
siamese_dataset = SiameseDataset(training_csv,training_dir,
transform=transforms.Compose([transforms.Resize((105,105)),
transforms.ToTensor()
])
)
# Load the dataset as pytorch tensors using dataloader
train_dataloader = DataLoader(
siamese_dataset, shuffle=True, num_workers=8, batch_size=config.batch_size
)
5.2 SNN model
Chúng ta sẽ tạo SNN model như sau:
#create a siamese network
class SiameseNetwork(nn.Module):
def __init__(self):
super(SiameseNetwork, self).__init__()
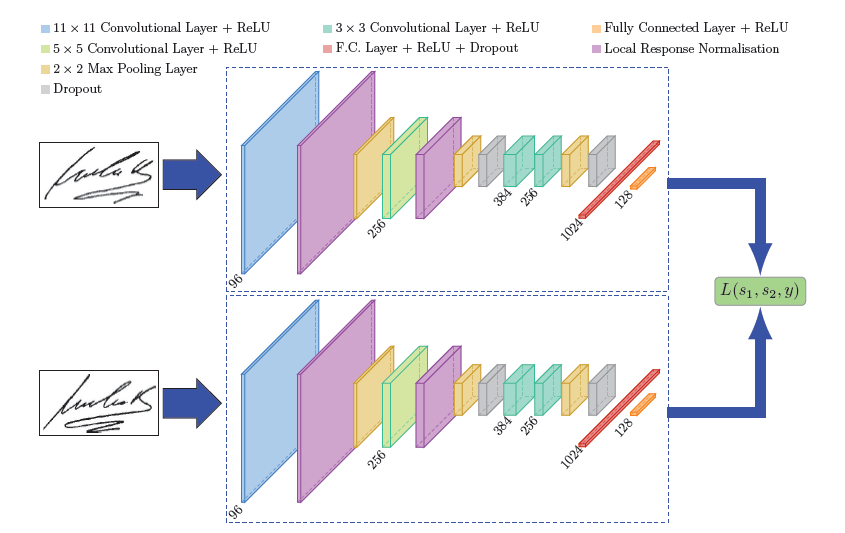
# Setting up the Sequential of CNN Layers
self.cnn = nn.Sequential(
nn.Conv2d(1, 96, kernel_size=11,stride=1),
nn.ReLU(inplace=True),
nn.LocalResponseNorm(5,alpha=0.0001,beta=0.75,k=2),
nn.MaxPool2d(3, stride=2),
nn.Conv2d(96, 256, kernel_size=5,stride=1,padding=2),
nn.ReLU(inplace=True),
nn.LocalResponseNorm(5,alpha=0.0001,beta=0.75,k=2),
nn.MaxPool2d(3, stride=2),
nn.Dropout2d(p=0.3),
nn.Conv2d(256,384 , kernel_size=3,stride=1,padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(384,256 , kernel_size=3,stride=1,padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(3, stride=2),
nn.Dropout2d(p=0.3),
)
# Defining the fully connected layers
self.fc = nn.Sequential(
nn.Linear(30976, 1024),
nn.ReLU(inplace=True),
nn.Dropout2d(p=0.5),
nn.Linear(1024, 128),
nn.ReLU(inplace=True),
nn.Linear(128,2))
def forward_once(self, x):
# Forward pass
output = self.cnn(x)
output = output.view(output.size()[0], -1)
output = self.fc(output)
return output
def forward(self, input1, input2):
# forward pass of input 1
output1 = self.forward_once(input1)
# forward pass of input 2
output2 = self.forward_once(input2)
return output1, output2
5.3 Loss Function
Trong bài này, mình sẽ sử dụng Contrastive Loss. Code của nó trong Pytorch như sau:
class ContrastiveLoss(torch.nn.Module):
"""
Contrastive loss function.
"""
def __init__(self, margin=1.0):
super(ContrastiveLoss, self).__init__()
self.margin = margin
def forward(self, x0, x1, y):
# euclidian distance
diff = x0 - x1
dist_sq = torch.sum(torch.pow(diff, 2), 1)
dist = torch.sqrt(dist_sq)
mdist = self.margin - dist
dist = torch.clamp(mdist, min=0.0)
loss = y * dist_sq + (1 - y) * torch.pow(dist, 2)
loss = torch.sum(loss) / 2.0 / x0.size()[0]
return loss
5.4 Train SNN model
Các bước tiến hành huấn luyện SNN model như sau:
- Khởi tạo model, Loss Funtion, và Optimizer (bài này sử dụng Adam)
- Đưa từng cặp Images vào SNN network.
- Tính toán Loss từ Ouput của mỗi ảnh.
- Tính toán Gradients của model theo phương pháp Back Propagate.
- Cập nhật các tham số của model, sử dụng Optimizer.
- Lưu lại model.
# Declare Siamese Network
net = SiameseNetwork().cuda()
# Decalre Loss Function
criterion = ContrastiveLoss()
# Declare Optimizer
optimizer = th.optim.Adam(net.parameters(), lr=1e-3, weight_decay=0.0005)
#train the model
def train():
loss=[]
counter=[]
iteration_number = 0
for epoch in range(1,config.epochs):
for i, data in enumerate(train_dataloader,0):
img0, img1 , label = data
img0, img1 , label = img0.cuda(), img1.cuda() , label.cuda()
optimizer.zero_grad()
output1,output2 = net(img0,img1)
loss_contrastive = criterion(output1,output2,label)
loss_contrastive.backward()
optimizer.step()
print("Epoch {}\n Current loss {}\n".format(epoch,loss_contrastive.item()))
iteration_number += 10
counter.append(iteration_number)
loss.append(loss_contrastive.item())
show_plot(counter, loss)
return net
#set the device to cuda
device = torch.device('cuda' if th.cuda.is_available() else 'cpu')
model = train()
torch.save(model.state_dict(), "output/model.pt")
print("Model Saved Successfully")
Kết quả huấn luyện sau 20 epochs:
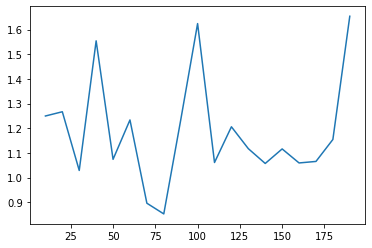
Giá trị của Loss vẫn còn dao động, có lẽ chúng ta phải Tuning model nhiều hơn. Trong bài này, mình ko đi chi tiết phần đó.
5.5 Test SNN model
Chúng ta sẽ thực hiện các bước sau để kiểm tra SNN model vừa mới huấn luyện:
- Đọc vào Test dataset, sử dụng lớp Dataloader của Pytorch
- Đưa cặp Image và nhãn tương ứng đi qua SNN model
- Tìm khoảng cách Euclidean giữa 2 Output
- Hiển thị kết quả
# Load the test dataset
test_dataset = SiameseDataset(training_csv=testing_csv,training_dir=testing_dir,
transform=transforms.Compose([transforms.Resize((105,105)),
transforms.ToTensor()
])
)
test_dataloader = DataLoader(test_dataset,num_workers=6,batch_size=1,shuffle=True)
#test the network
count=0
for i, data in enumerate(test_dataloader,0):
x0, x1 , label = data
concat = torch.cat((x0,x1),0)
output1,output2 = model(x0.to(device),x1.to(device))
eucledian_distance = F.pairwise_distance(output1, output2)
if label==torch.FloatTensor([[0]]):
label="Original Pair Of Signature"
else:
label="Forged Pair Of Signature"
imshow(torchvision.utils.make_grid(concat))
print("Predicted Eucledian Distance:-",eucledian_distance.item())
print("Actual Label:-",label)
count=count+1
if count ==10:
break
Kết quả:
Predicted Eucledian Distance:- 1.2930774688720703
Actual Label:- Forged Pair Of Signature
Predicted Eucledian Distance:- 0.6725202798843384
Actual Label:- Original Pair Of Signature
Predicted Eucledian Distance:- 0.8823959827423096
Actual Label:- Forged Pair Of Signature
Predicted Eucledian Distance:- 0.9346675276756287
Actual Label:- Forged Pair Of Signature
Predicted Eucledian Distance:- 0.25577670335769653
Actual Label:- Forged Pair Of Signature
Predicted Eucledian Distance:- 0.7937518358230591
Actual Label:- Forged Pair Of Signature
Predicted Eucledian Distance:- 0.7733522057533264
Actual Label:- Original Pair Of Signature
Predicted Eucledian Distance:- 0.7810924649238586
Actual Label:- Original Pair Of Signature
Predicted Eucledian Distance:- 1.2326889038085938
Actual Label:- Original Pair Of Signature
Predicted Eucledian Distance:- 0.6290231347084045
Actual Label:- Original Pair Of Signature
Một số hình ảnh:

6. Kết luận
Trong bài này, chúng ta đã cùng tìm hiểu về Siamese Neural Network, đồng thời xây dựng một SNN đơn giản để giải quyết bài toán Signature Verification.
Toàn bộ source code của bài này, các bạn có thể tham khảo tại đây
Trong bài tiếp theo, chúng ta sẽ cùng thảo luận về cách thức xây dựng và tổ chức Source Code trong các dự án về AI. Mời các bạn đón đọc.
7. Tham khảo