Các phương pháp Optimization - Gradient Descent
“Nearly all of deep learning is powered by one very important algorithm: Stochastic Gradient Descent (SGD)” – Goodfellow et al.
Từ bài trước chúng ta đã biết rằng để model có thể dự đoán đúng thì phải tìm được giá trị phù hợp cho $W$ và $b$. Nếu chúng ta chỉ dựa hoàn toàn vào việc chọn ngẫu nhiên thì gẫn như không bao giờ có thể tìm được giá trị mong muốn. Thay vì thế, chúng ta cần định nghĩa một thuật toán tối ưu (optimization) và sử dụng nó để cải thiện $W$ và $b$. Trong bài này, chúng ta sẽ tìm hiểu một thuật toán tối ưu được sử dụng rất rất phổ biến trong NN and DL model - Gradient Descent (GD) và các biến thể của nó. Ý tưởng chung của họ các thuật toán GD là đánh giá các tham số, tính toán loss, sau đó thực hiện một bước nhỏ theo hướng giảm loss. Cả 3 bước này được thực hiện trong các vòng lặp cho đến khi gặp một điều kiện dừng nào đó.
1. The Loss Landscape và Optimization Surface
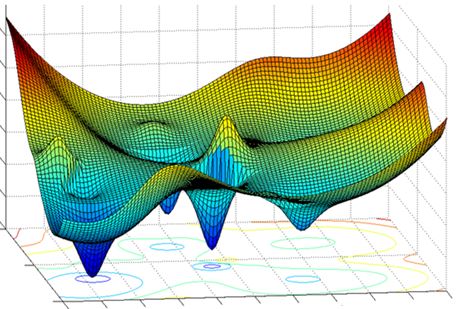
Gradient descent là thuật toán hoạt động theo kiểu tối ưu qua từng vòng lặp thông qua một mặt tối ưu(optimization surface / loss landscape), như minh họa ở hình bên dưới.

Phía bên trái biểu diễn trong không gian 2 chiều để chúng ta dễ hình dùng, còn bên phải biểu diễn một cách thực tế hơn trong không gian nhiều chiều. Mục đích sử dụng gradient descent là tìm ra điểm global minumum (đáy của cái bát ở bên phải).
Chúng ta có thể thấy, optimization surface có rất nhiều đỉnh (peaks) và thung lũng (valleys*). Mỗi valley có một điểm đáy mà tại đó giá trị loss đạt giá trị cực tiểu, gọi là local minimum. Trong số các điểm local minimum, có 1 điểm mà giá trị loss đạt giá trị nhỏ nhất được gọi là gloabal minimum. Đây chính là điểm mà chính ta muốn tìm trong quá trình training AI model thông qua việc cập nhật các tham số.
Hãy tưởng tượng, việc dò tìm điểm global minimum trên optimization surface giống như việc đặt 1 viên bi (*chính là * $W$) trên mặt đó, nhiệ vụ của viên bi là dò tìm đường để đi đến điểm đích (global minimum).
Nếu chỉ nhìn vào hình trên, mọi người có thể thắc mắc: Nếu muốn đến điểm global minimum, tại sao không nhảy thẳng một phát đến đó?
Nhưng mọi việc không đơn giản như vậy, bởi vì trên thực tế, chúng ta không biết hình dạng của optimization surface như thế nào, chúng ta như một ngươi mù trên đường, không biết phương hướng. Và các thuật toán tối ưu (gradient descent là một trong số đó) chính là cây gậy trong tay, giúp chúng ta dò đường.
Cụ thể hơn 1 chút thì mỗi một điểm trên optimization surface tương ứng với một giá trị loss $L$ - chính là output của loss funtion khi đưa vào cặp giá trị ($W$, $b$). Ý tưởng của thuật toán tối ưu là cố gắng thử sử dụng các cặp giá trị ($W$, $b$) khác nhau, tính toán loss, cập nhật ($W$, $b$) sao cho giá trị loss thấp hơn … Lý tưởng nhất là chúng ta có thể đạt được giá trị loss nhỏ nhất tại điểm global minimum, nhưng điều này thường khó xảy ra trong thực tế.
2. Gradient Descent cho hàm 1 biến
Giả sử Loss Function của chúng ta là hàm bậc 1, $f(x)$. Điểm global minimum là điểm mà tại đó $x = x^*$.
Đạo hàm của của $f(x)$ là $f'(x)$. Nếu bạn còn nhớ, trong chương trình toán THPT, khi học về đạo hàm ta có các nhận xét:
- Nếu đạo hàm của hàm số tại thời điểm $t$, $f'(x_t) > 0$ thì $x_t$ nằm về phía bên phải so với $x^*$, và ngược lại.
- $x_t$ càng xa $x^*$ về phía bên phải thì $f'(x_t)$ càng lơn hơn 0, và ngược lại.
Từ nhận xét số 1 có thể suy ra, để điểm tiếp theo $x_{t+1}$ tiến gần về $x^*$ hơn thì cần di chuyển $x_t$ về phía bên trái, tức là phía âm, hay phía ngược dấu với đạo hàm:
Từ nhận xét số 2 có thể suy ra lượng di chuyển $\Delta$ tỉ lệ thuận với $-f'(x)$.
Tổng hợp hai nhận xét trên, ta có công thức cập nhật $x_t$ một cách đơn giản là:
Hoặc viết dưới dạng đơn giản:
Trong $\eta$ là một số > 0, gọi là learning rate. Dấu trừ thể hiện viêc đi ngược chiều với đạo hàm (descent nghĩa là đi ngược).
3. Gradient Descent cho hàm nhiều biến
Giả sử Loss Function của chúng ta, $f(\theta)$ là hàm nhiều biến, trong đó $\theta$ là tập hợp các vector các tham số của model cần tối ưu. Đạo hàm của $f(\theta)$ tại thời điểm $\theta$ là $\nabla_\theta f(\theta)$.
Tương tự hàm 1 biến, quy tắc cập nhật $\theta$ là:
Hoặc viết dưới dạng đơn giản:
Tóm lại, thuật toán GD hoạt động như sau:
- Dự đoán một điểm khởi tạo $\nabla = \nabla_0$.
- Cập nhật $\nabla$ đến khi đạt được kết quả chấp nhận được (hoặc một điều kiện dừng nào đó).
$\theta = \theta - \eta \nabla_\theta f(\theta)$
với $\nabla_\theta f(\theta)$ là đạo hàm của Loss Function tại $\theta$.
4. Stochastic Gradient Descent (SGD)
Thuật toán GD nguyên thủy có một nhược điểm to lớn là hội tụ rất chậm và yêu cầu tài nguyên tính toán rất lớn. Nguyên nhân gốc rễ của vấn đề này là do GD tính toán gradient trên toàn bộ training set. Điều này thật khó để chấp nhận nếu áp dụng với một tập dữ liệu lớn.
Một biến thể của GD, gọi là Stochastic Gradient Descent (SGD) ra đời, khắc phục những hạn chế của GD. Thay vì tính toán và cập nhật weight matrix $W$ trên toàn bộ tập dữ liệu như cách làm của GD (cập nhật theo epoch), SGD chia nhỏ tập training thành các batchs (dữ liệu thường được xáo trộn ngẫu nhiên trước khi chia), tính toán và cập nhật $W$ theo từng batch đó (cập nhật theo batch).
Biểu diễn theo toán học, công thức cập nhật của SGD như sau:
trong đó, $f(\theta;x_i;y_i)$ là Loss Function với chỉ 1 cặp điểm dữ liệu (input, label) là ($x_i, y_i$).
Mặc dù ra đời từ rất lâu (1960), SGD vẫn là một thuật toán quan trọng, được sử dụng rộng rãi trong các kiến trúc DL hiện đại. Vì thế, viêc hiểu cặn cẽ về nó là một điều cần thiết khi học AI/ML.
4.1 Mini-batch SGD
Một câu hỏi đặt ra khi sử dụng SGD là kích thước của batch (batch_size) là bao nhiêu thì hợp lý? Theo như cách diễn giải bên trên thì có vẻ như batch_size càng nhỏ càng tốt? Và tốt nhất là batch_size = 1?
Tuy nhiên, điều này không đúng. Sử dụng batch_size > 1 mang lại cho chúng ta một số lợi ích nhất định. Nó giúp giảm phương sai khi cập nhật $W$, và đặc biệt hơn, nếu giá trị của batch_size là lũy thừa của 2 thì chúng ta còn hưởng lợi về tốc độ thực thi của các thư viện tối ưu trong đại đố tuyến tính. Trong các bài toán thực tế, batch_size thường nhận các giá trị 32, 64, 128, 256, tùy thuộc vào tài nguyên tính toán của bạn.
Lúc này, công thức cập nhật sẽ trở thành:
trong đó, $x_{i:i+n}, y_{i:i+n}$ là các cặp điểm dữ liệu (*input, label*) có vị trí từ $i$ đến $i + n -1$.
4.2 Mở rộng của SGD
Trong quá trình sử dụng SGD, ta có thể bắt gặp 2 kỹ thuật hỗ trợ tăng tốc độ hội tụ cho SGD. Đố là momentum và nesterov accelerated gradient (NAG).
4.2.1 Momentum
Momentum, hiểu theo nghĩa tiếng việt là đà, lấy đà hay quán tính. Mục tiêu của nó là đẩy nhanh tốc độ cập nhật $W$ tại những nơi mà các gradients có cùng hướng, và ngược lại. Quan sát lại hình bên trên, có thể tưởng tượng rằng nếu không có momentum, viên bi của chúng ta rất dễ bị mắc kẹt ở các local minimum, mà không sao thoát ra để tìm đến global minimum được.
Ở phần trên, ta đã biết công thức cập nhật các tham số như sau:
Thêm vào momentum $V$, với:
ta được:
Trong đó, $\gamma$ là đại lượng thường được chọn giá trị 0.9, hoặc ban đầu chọn là 0.5, sau khi quá trình học diễn ra ổn định thì tăng lên 0.9. Nó hầu như không bao giờ < 0.5. Khi khai báo sử dụng momentum (trong tensorflow chẳng hạn), ta thường truyền vào giá trị của đại lương này.
4.2.2 Nesterov Accelerated Gradient (NAG)
Momentum tuy giúp ta vượt qua được các local minimum, nhưng khi tới gần global minimum, do có đà nên viên bi vẫn tiếp tục dao động thêm một khoảng thời gian nữa mới có thể dừng lại đúng điểm cần dừng. NAG ra đời để khắc phục nhược điểm này.
Ý tưởng chính của NAG là sử dụng gradient ở thời tiếp theo, thay vì gradient ở thời điểm hiện tại khi tính lượng thay đổi của $\theta$.
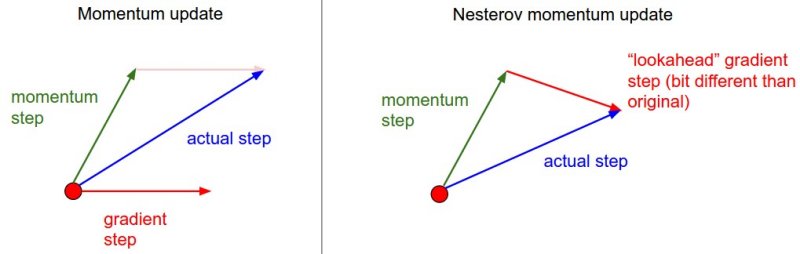
Ý tưởng của Nesterov accelerated gradient.
Nguồn: CS231n Stanford: Convolutional Neural Networks for Visual RecognitionCông thức cập nhật sẽ như sau:
Momentum là một kỹ thuật quan trọng và hiệu quả, gần như luôn luôn được sử dụng cùng với SGD. Còn đối với NAG, chúng ta ít gặp hơn. Trong khi về mặt lý thuyết, nó mang lại hiệu quả hơn momentum, nhưng trong thực tế các kiến trúc nổi tiếng như AlexNet, VGGNet, ResNet, Inception, … khi train trên tập dữ liệu ImageNet, chỉ sử dụng SGD với momentum. Có lẽ NAG chỉ phù hợp với các tập dữ liệu nhỏ.
5. Các thuật toán tối ưu khác
Ngoài SGD, hai thuật toán khác cũng rất hay được sử dụng trong các kiến trúc DL hiện đại là Adam và RMSprop. Mình sẽ có bài viết riêng về các thuật toán này. Mời các bạn đón đọc.
Tham khảo