Mạng thần kinh tích chập (Convolutional Neural Network (CNN) - Phần 2
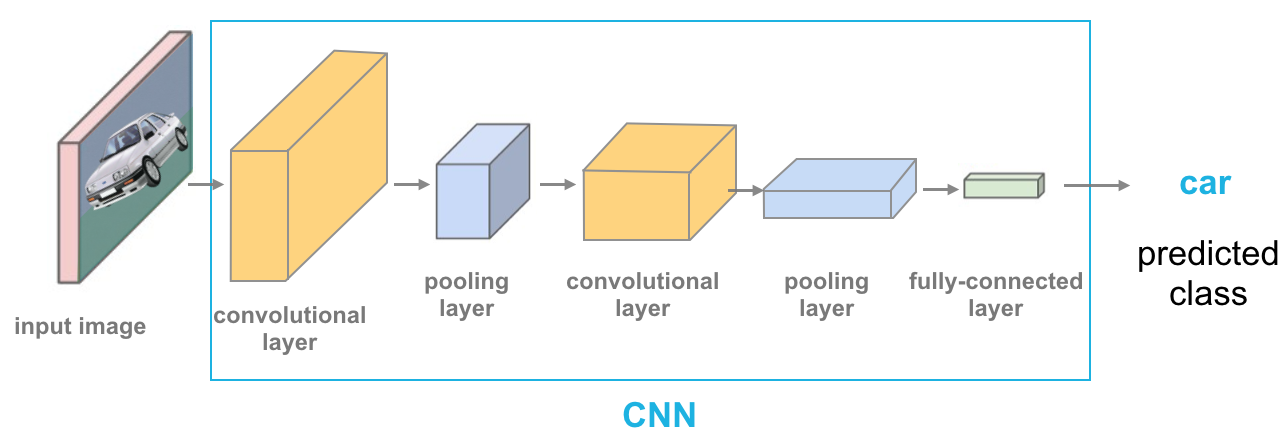
Vì sử dụng trực tiếp raw pixel của image nên so với CNN, FCN (Fully Connected Network) có 2 nhược điểm kích thước của image tăng lên:
- Hiệu năng giảm mạnh.
- Kích thước của mạng tăng nhanh.
Kết quả thực nghiệm cho thấy, khi áp dụng
Fully Connected Networkvào bộ dataset CIFAR-10, độ chính xác chỉ đạt được 52%.
CNN, theo một cách khác, sắp xếp các layers theo dạng 3D volume với 3 chiều: Width, Height, Depth. Các neurons trong mỗi layer chỉ kết nối tới 1 small region của layer trước đó - gọi là local connectivity. Điều này giúp giảm bớt rất nhiều kích thước của mạng.
2. Các loại layers
Có khá nhiều các dạng layers khác nhau để xây dựng nên CNNs. Các loại dưới đây được sử dụng phổ biến:
- Convolutional (CONV)
- Activation (ACT, RELU, SOFTMAX)
- Pooling (POOL)
- Fully-connected (FC)
- Batch normalization (BN)
- Dropout (DO)
Sắp xếp các dạng layers trên liên tiếp nhau theo thứ tự nào đó sẽ cho ta một CNN.
Ví dụ: INPUT => CONV => RELU => FC => SOFTMAX
Ở đây, ta định nghĩa một CNN đơn giản, nhận input, áp dụng “convolution layer”, sau đó là 1 “activation layer” (RELU), tiếp theo là 1 “fully-connected layer”. Cuối cùng là một “activation layer” nữa (SOFTMAX) để đạt được xác suất của output theo các nhãn cần phân loại.
Trong số các lớp trên, chỉ có CONV và FC là chứa các tham số được cập nhật trong quá trình training. POOL có tác dụng thay đổi kích thước không gian của image khi nó di chuyển qua các lớp của CNN.
CONV, POOL, RELU và FC là 4 layers quan trọng nhất, gần như không thể thiếu khi xây dựng CNNs.
2.1 CONV
CONV chứa một tập K learnable filters (ví dụ: Kernel), mỗi filter có kích thước width x height. Mặc định,width luôn luôn bằng height, trừ khi có lý do đặc biệt. Hai giá trị này có thường nhỏ (1, 3, 5, 7) nhưng K thì có thể rất lớn (4, 8, 16, 32, 64, 128, …). K cũng được gọi là độ sâu (depth) của CONV layer.
Cùng xem xét forward-pass của một CNN. CONV có K filters, áp dụng vào một input volumn có kích thước WxH. Tưởng tượng rẵng, mỗi filters sẽ trượt ngang qua toàn bộ input volumn, tính toán convolution, sau đó lưu kết quả ra một mảng 2 chiều, gọi là activation map. Xem hình bên dưới:
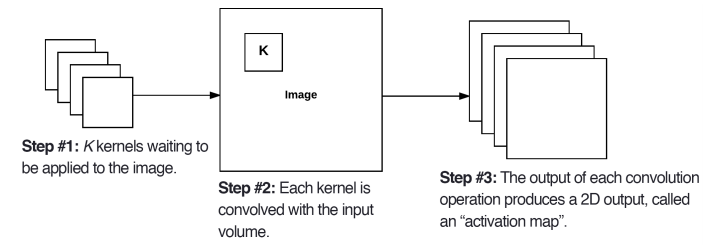
Sau khi áp dùng K filters lên input volumn, chúng ta thu được K, 2-dimensional activation maps. Xếp chồng (Stack) những activation maps này theo chiều sâu sẽ thu được kết qủa cuối cùng (output volumn).

Xét về kích thước của output volumn, có 3 tham số tác động. Chúng là depth, stride và zero-padding size.
- Depth
Như đã nói ở trên, depth chính là số lượng filters trong CONV layer, có giá trị là K.
- Stride
Stride là kích thước của step khi các filters trượt qua input volumn. Giá trị của stride thường là 1 hoặc 2 (S=1 hoặc S=2), tương ứng với step là 1 hoặc 2 pixel. S nhỏ sẽ sinh ra ouput volumn lớn, và có nhiều vùng được bị trùng lặp trong quá trình trượt và tính covolution của các filters. Đối với S lớn, kết quả sẽ ngược lại.
Xem ví dụ sau:
Trong hình bên dưới, ma trận bên trái là input volumn, ma trận bên phải là filter.
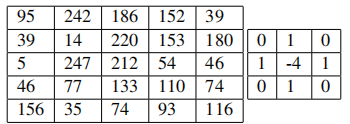
Sử dụng S = 1 và S = 2 cho convolution, thu được kết quả tương ứng bên trái, phải trong hình sau:

Cùng với pooling (xem phần bên dưới), stride có thể được sử dụng để giảm kích thước của input volumn.
- Zero-padding
Sử dụng stride làm giảm kích thước của input volumn. Vậy nếu muốn giữ nguyên kích thước của input volumn thì sao? Zero-padding chính là câu trả lời.
Zero-padding tức là gắn thêm (pad) viền (border) cho input volumn. Các giá trị được gắn thêm đều là 0, vì thế mà có tên zero-padding.
Xem ví dụ sau:
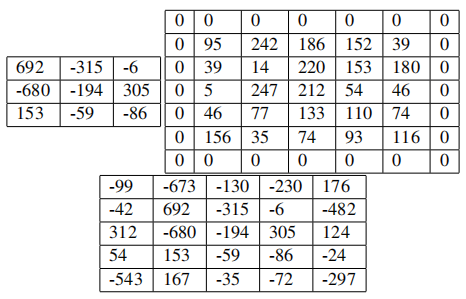
Bên trái là 3x3 ouput khi áp dụng 3x3 convolution tới 5x5 input.
Bên phải là khi áp dụng zero-padding vào input, thu được input mới có kích thước 7x7. Giá trị của zero-padding trong trường hợp này là P = 1.
Bên dưới là 5x5 ouput khi áp dụng 3x3 convolution tới 7x7 input. Ta thấy kích thước 5x5 của input ban đầu được duy trì trong output.
Nếu không sử dụng zero-padding, kích thước của input volumn sẽ giảm rất nhanh, do đó không thể xây dựng CNN nhiều layers.
Công thức tính kích thước của ouput volumn như sau: O = ((W - F + 2P)/S) + 1
Trong đó:
- 0: kích thước của output volumn.
- W: kích thước input volumn
- F: kích thước của filter
- P: kích thước zero-padding
- S: kích thước stride
Nếu O không phải là số nguyên, cần thay đổi lai giá trị của S.
Thử áp dụng công thức này vào ví dụ bên trên:
O = ((5 - 3 + 2*1)/1) = 5
2.2 Activation Layers
Activation layer thường được áp dụng sau mỗi CONV layer trong một mạng CNN. Các activation layer hay dùng là các hàm phi tuyến, giống như: ReLU, ELU, Leaky ReLU. Trong các public paper, ReLU được sử dụng rất phổ biến, gần như là mặc định. Khi viết ACT, ta ngầm hiểu đó là ReLU.
Trên thực tế, activation layer không được coi là một layer theo đúng nghĩa. Bởi vì nó không có parameters nào được học trong quá trình huấn luyện mô hình. Trong một số diagram kiến trúc của mạng, nó có thể không xuất hiện và được ngầm hiểu rằng nó nằm ngay sau CONV layer.
Ví dụ với kiến trúc sau:
INPUT => CONV => RELU => FC
Có thể được viết gọn thành:
INPUT => CONV => FC
Một activation layer nhận input volumn có kích thước là $W_{input}$x$H_{input}$x$D_{input}$, áp dụng activation function theo kiểu element-wise nên kích thước của output volumn đúng bằng kích thước của input volumn: $W_{input}$=$W_{output}$, $H_{input}$=$H_{output}$, $D_{input}$=$D_{output}$.
2.3 Pooling Layers
Có 2 phương pháp để giảm kích thước của input volumn: CONV layer (với stride > 1) và POOL layer.
Thông thường, POOL layer được đặt ngay sau ACT layer và trước CONV layer. Trong trường hợp không có ACT layer thì nó nằm giữa 2 CONV layer.
Ví dụ kiến trúc mạng sau:
INPUT => CONV => RELU => POOL => CONV => POOL => FC
Chức năng đầu tiên của POOL layer là giảm kích thước không gian của input volumn một các từ từ. Điều này dẫn đến việc giảm số lượng tham số và sự phức tạp tính toán của mạng. Vì thế mà nó là một trong những phương pháp hiệu của để tránh hiện tượng Overfitting cho mạng DL.
POOL layer hoạt động độc lập trên mỗi depth slice của input volumn, sử dụng hàm max hoặc average. Hai cái tên có lẽ cũng đã nói lên cách thức hoạt động của chúng. Max pooling chỉ giữ lại giá trị lớn nhất trong phạm vi kích thước của nó còn average pooling thì lấy giá trị trung bình của các giá trị trong phạm vi kích thước của POOL layer. Về vị trí trong kiến trúc, trong khi max pooling thường được đặt ở giữa của kiến trúc mạng DL để giảm kích thước, còn average pooling lại hay được đặt ở các layers cuối (hoặc gần cuối) (VD: GoogLeNet, SqueezeNet, ResNet) để thay thế cho các FC layers, giúp giảm độ phức tạp cả model.
Kích thước của POOL layer hay được sử dụng là 2x2. Mặc dù vậy, với input volumn có kích thước > 200x200, ta có thể sử dụng kích thước 3x3 của POOL ở những layer đầu.
Bước nhảy (stride, S) của mỗi POOL layer thường là 1 hoặc 2. Hình bên dưới minh họa kết quả hoạt dộng của max pooling với S =1,2, tương ứng.
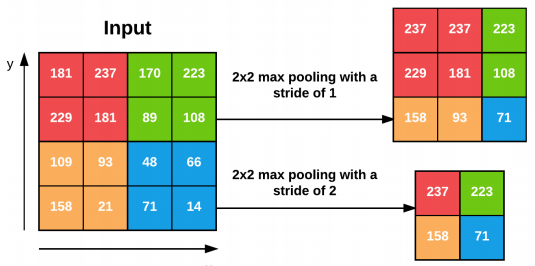
Công thức tính kích thước của output volumn sau khi qua POOL layer như sau:
- $W_{output}$ = (($W_{input}$ - $F$)/$S$) + 1
- $H_{output}$ = (($H_{input}$ - $F$)/$S$) + 1
- $D_{output}$ = $D_{input}$
Trong đó:
- $W_{input}$x$H_{input}$x$D_{input}$: kích thước của input volumn.
- $W_{output}$x$H_{output}$x$D_{output}$: kích thước của output volumn.
- F: kích thước của POOL layer (cũng gọi là
pool size). - S: stride
Trong các bài toán thực tế, có 3 dạng max pooling thường hay được sử dụng.
- Dạng 1: (F = 3, S = 2), gọi là
overlapping pooling, thường áp dụng đối với các images/input volumn có kích thước lớn (> 200x200 pixels) - Dạng 2: (F = 2, S = 2), gọi là
non-overlapping pooling, thường được áp dụng với các images/input volumn có kích thước trung bình (> 64x64 pixels và < 200x200 pixels) - Dạng 3: (F = 2, S = 1), gọi là
small pooling, áp dụng với các images/input volumn nhỏ (< 64x64 pixels)
Đến đây, có thể các bạn sẽ thắc mắc, khi nào thì dùng CONV layer, khi nào thì dùng POOL layer để giảm kích thước của input volumn?
Springenberg et al, trong paper Striving for Simplicity: The All Convolutional Net xuất bản năm 2014 của họ đã đề xuất loại bỏ hoàn toàn POOL layer, chỉ sử dụng CONV layer (với S>1). Họ đã chứng minh tính hiệu của cách tiếp cận này trên một số tập dữ liệu, bao gồm cả CIFAR-10 (small images, low number of class) và ImageNet (large input images, 1000 classes). Xu hướng này cũng xuất hiện trong kiến trúc của mạng Resnet năm 2015 và đang dần dần trở nên phổ biến hơn. Có lẽ trong tương lai không xa, chúng ta sẽ không sử dụng POOL layer (cụ thể là max pooling) trong phần giữa các kiến trúc mạng DL hiện đại nữa mà chỉ sử dụng average pooling tại các layer cuối để thay thế cho FC layer vốn cồng kềnh và phức tạp. Tuy nhiên, trước mắt thì max pooling vẫn chưa thể biến mất hoàn toàn được, nên chúng ta vẫn cần phải học, hiểu và áp dụng chúng trong việc xây dựng kiến trúc mạng DL của riêng mình, cũng như đọc hiểu các kiến trúc mạng DL kinh điển khác.
2.4 Full-Connected (FC) Layers
FC Layer chính là Feedforward Neural Network mà chúng ta đã tìm hiểu trong bài …. Nó luôn được đặt ở cuối trong các kiến trúc mạng DL.
Ví dụ kiến trúc mạng sau,
INPUT => (CONV => RELU => POOL)x2 => FC => FC => SOFTMAX.
ta đã sử dụng 2 FC layers ở gần cuối mạng, theo sau là ACT layer (SOFTMAX) để phân loại (tính toán xác suất của mỗi classes).
2.5 Batch Normalization (BN)
Được giới thiệu lần đầu vào năm 2015 trong paper Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift của Ioffe và Szegedy, BN đã nhanh chóng trở nên phổ biến trong các kiến trúc mạng DL. Đúng như tên của nó, BN layer có tác dụng normalize input volumn trước khi đi vào layer tiếp theo.
Giả sử, ta có input tại thời đểm i (mini-batch i) là $x_i$, sau khi đi qua BN layer, ta thu được giá trị $\widehat{x_i}$ theo công thức:
- Trong đó:
-
$\mu_ \beta = \frac{1}{M}\sum_{i=1}^m x_i$
-
$\sigma^2_ = \frac{1}{M}\sum_{i=1}^m (x_i - \mu_\beta)^2$
-
Giá trị của $\varepsilon$ được chọn là giá trị dương đủ nhỏ (VD: 1e-7) để tránh việc chia cho 0. Sau khi áp dụng BN, input volumn sẽ có trung bình (mean) xấp xỉ 0 và độ lệch chuẩn (variance) xấp xỉ 1 (còn gọi là zero-centered).
Khi sử dụng model để test, ta thay thế $\mu_\beta$ và $\sigma_\beta$ bằng giá trị trung bình của chúng trong suốt quá trình training. Điều này đảm bảo cho ta có thể pass input volumn xuyên qua mạng DL mà không bị biased bởi giá trị $\mu_\beta$ và $\sigma_\beta$ tại thời điểm cuối cùng ($x_m$).
BN layer tỏ ra hiệu quả cao trong việc làm cho quá trình training một NN ổn định hơn, giảm số lượng epochs cần thiêt để train model, và quan trọng nhất là hạn chế tình trạng Overfitting. Khi sử dụng BN, việc tuning các tham số khác của model cũng trở nên đơn giản hơn bởi vì BN đã thu hẹp đáng kế phạm vi giá trị của các weights trong mạng.
Hạn chế lớn nhất của BN có lẽ là nó làm tăng thời gian training của bạn do phải tính toán normalization và statistic tại mỗi nơi mà nó xuất hiện trong kiến trúc mạng. Thường là tăng gấp 2 đến 3 so với không sử dụng BN.
Tuy nhiên, có lẽ hạn chế trên không đáng kể so với những ưu điểm mà BN mang lại. Vì vậy, lời khuyên ở đây là nên sử dụng BN thường xuyên trong bài toán của bạn.
Cuối cùng là về vị trí đạt BN layer trong kiến trúc DL. Mặc dù trong paper gốc của tác giả BN layer được đặt trước ACT layer, nhưng điều này lại không hợp lý vê mặt thống kê. Bởi vì output của BN là zero-centered, khi đi qua ACT layer (ReLU), phần giá trị âm sẽ bị triệt tiêu. Điều này vô tình làm mất đi bản chất của BN. Thực nghiệm rất nhiều cũng đã chỉ ra rằng, đặt BN layer ở sau ACT layer cho kết quả tốt hơn (higher accuracy và lower loss) trong hầu hết mọi trường hợp. Vì thế, mặc định, hãy đặt BN layer sau ACT layer, trừ khi bạn có lý do đặc biệt nào khác.
Ví dụ về việc đặt BN layer trong kiến trúc DL:
INPUT => CONV => RELU => BN …
2.6 Dropout (DO) layer
DO thực chất là một dạng của regularization, mục đích là để hạn chế hiện tượng Overfitting. Tại mỗi mini-batch trong quá trình train, DO layer sẽ ngẫu nhiên ngắt kết nối các inputs giữa 2 layer liên tiếp, với xác suất p.
Ví dụ về DO với p = 5 giữa 2 FC layers như hình bên dưới:

DO chỉ hoạt động theo 1 chiều forwarding, chiều ngược lại (backwarding), các dropped connections sẽ được kết nối lại để tính toán.
DO giúp giảm Overfitting theo cách như trên bởi vì khi đó, vai trò của các nodes trong mạng sẽ được phân phối đều hơn, không có nodes nào chịu trách nhiệm chính, nhiều hơn các nodes khác. Điều này sẽ giúp model generalize tốt hơn.
Về vị trí trong kiến trúc mạng DL, DO layer thường được set với p = 0.5 và đặt xen kẽ 2 FC layers ở cuối.
Ví dụ:
INPUT => CONV => RELU => POOL => FC => DO => FC => DO => SOFTMAX
Bài thứ 2 về CNN xin được kết thúc tại đây. Trong bài tiếp theo (cũng là bài cuối cùng về CNN), mình sẽ chia sẻ một số patterns và một số rules trong việc xây dựng kiến trúc CNN. Mời các bạn đón đọc!
Tham khảo