Neural Network cơ bản (Phần 2)
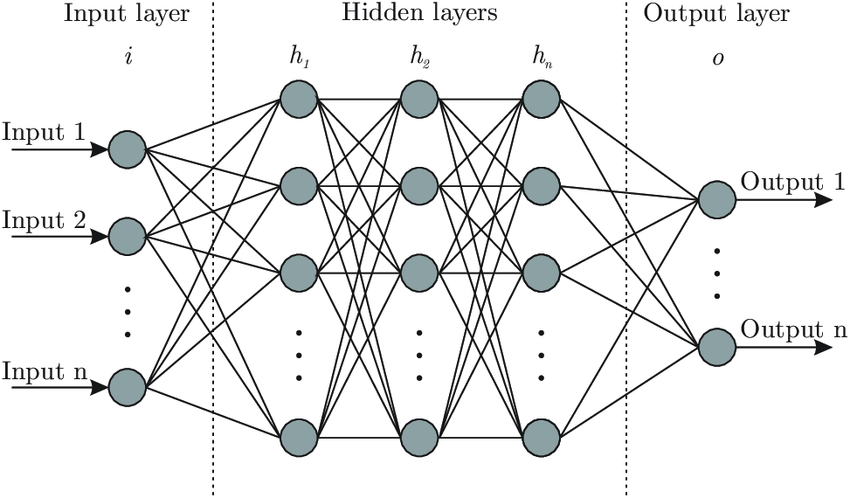
Trong quá trình tìm hiểu về mạng NN, mình thấy khá là khó hiểu, đặc biệt với các bạn không mạnh về toán. Bài này, mình sẽ diễn giải cách thức làm việc của NN một cách trực quan, dễ hiểu cho các bạn thông qua một ví dụ cụ thể.
1. Nhắc lại lý thuyết
Giả sử ta có mạng NN như sau:
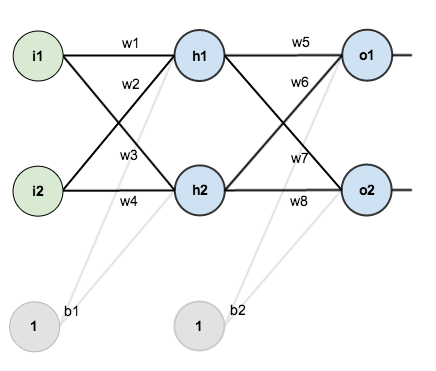
Quá trình training model bao gồm 2 phases:
1.1 Forward Path
Phase này tính toán (dự đoán) đầu ra $o_1, o_2$, tính loss.
Giả sử activation là hàm sigmoid:

Ta sẽ tính lần lượt các đại lượng trung gian:
- $in_{h_1}$: input của $h_1$
- $in_{h_2}$: input của $h_2$
- $out_{h_1}$: output của $h_1$
- $out_{h_2}$: output của $h_2$
- $in_{o_1}$: input của $o_1$
- $in_{o_2}$: input của $o_2$
- $out_{o_1}$: output của $o_1$
- $out_{o_2}: output của $o_2$$
Công thức tính của từng đại lượng như sau:
$in_{h_1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1$
$in_{h_2} = w_3 * i_1 + w_4 * i_2 + b_1 * 1$
$out_{h_1} = sigmoid(in_{h_1}) =$$\frac{1}{1 + e^{-in_{h_1}}}$
$out_{h_2} = sigmoid(in_{h_2}) =$$\frac{1}{1 + e^{-in_{h_2}}}$
$in_{o_1} = w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1$
$in_{o_2} = w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1$
$out_{o_1} = sigmoid(in_{o_1}) =$$\frac{1}{1 + e^{-in_{o_1}}}$
$out_{o_2} = sigmoid(in_{o_2}) =$$\frac{1}{1 + e^{-in_{o_2}}}$
Tiếp theo là tính loss bằng cách so sánh đầu ra của mạng NN với các giá trị thực tế:
- $target_{o_1}$
- $target_{o_2}$:
Công thức tính loss như sau:
$E_{total} = \sum_{i=1}^2 E_{o_i} = \sum_{i=1}^2 \frac{1}{2} (target_{o_i} - out_{o_i})^2 = E_{o_1} + E_{o_2}$
$E_{o_1} = \frac{1}{2} (target_{o_1} - out_{o_1})^2$
$E_{o_2} = \frac{1}{2} (target_{o_2} - out_{o_2})^2$
1.2 Backward Path
Mục đích của phase này là cập nhật trọng số $w$ sao cho tối thiểu hóa loss.
Ta sẽ sử dụng thuật toán tối ưu Stochastic Gradient Descent (SGD) để cập nhật $w$.
Công thức cập nhật như sau:
với:
- $\nabla_\theta f(\theta)$ là đạo hàm của Loss Function tại $\theta$ (đạo hàm từng phần theo $\nabla$).
- $\eta$ là một số > 0, gọi là
learning rate. - $\theta$ là tập hợp các vector các tham số của model cần tối ưu. Trong trường hợp này là các trọng số $w$.
Đạo hàm từng phần của các $w$ tại output layer được tính theo quy tắc chain rule như sau:
$\frac{\partial E_{total}}{\partial w_5} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_5}$
$\frac{\partial E_{total}}{\partial w_6} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_6}$
$\frac{\partial E_{total}}{\partial w_7} = \frac{\partial E_{total}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial w_7}$</p>
$\frac{\partial E_{total}}{\partial w_8} = \frac{\partial E_{total}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial w_8}$
Đạo hàm từng phần của các $w$ tại hidden layer được tính như sau:
$\frac{\partial E_{total}}{\partial w_1} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_1}$
$\frac{\partial E_{total}}{\partial w_2} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_2}$
$\frac{\partial E_{total}}{\partial w_3} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_3}$
$\frac{\partial E_{total}}{\partial w_4} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_4}$
Sau khi tính được đạo hàm từng phần của mỗi $w$, ta áp dụng công thức phía trên để cập nhật $w$.
2. Ví dụ áp dụng
Vẫn với kiến trúc mạng như trên, ta sẽ gán các giá trị khởi tạo cho các tham số như hình bên dưới:
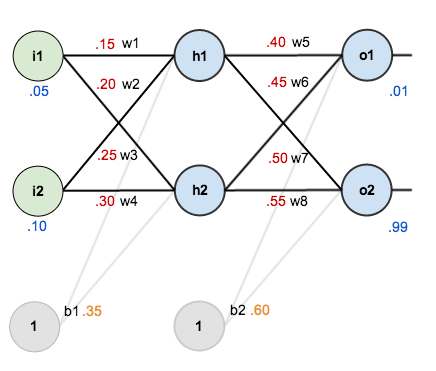
Ok, bây giờ ta sẽ bắt đầu đi tính toán.
2.1 Fordward Path
Input của $h_1$:
$in_{h_1} = w_1 * i_1 + w_2 * i_2 + b_1 * 1$
$in_{h_1} = 0.15 * 0.05 + 0.2 * 0.1 + 0.35 * 1$
$in_{h_1} = 0.3775$
Input của $h_2$:
$in_{h_2} = w_3 * i_1 + w_4 * i_2 + b_1 * 1$
$in_{h_2} = 0.25 * 0.05 + 0.3 * 0.1 + 0.35 * 1$
$in_{h_2} = 0.3925$
Ouput của $h_1$:
$out_{h_1} = $ $\frac{1}{1 + e^{-in_{h_1}}}$
$out_{h_1} = \frac{1}{1 + e^{-0.3775}}$
$out_{h_1} = 0.593269992$
Output của $h_2$:
$out_{h_2} = $ $\frac{1}{1 + e^{-in_{h_2}}}$
$out_{h_2} = \frac{1}{1 + e^{-0.3925}}$
$out_{h_2} = 0.596884378$
Input của $o_1$:
$in_{o_1} = w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1$
$in_{o_1} = 0.4 * 0.593269992 + 0.45 * 0.596884378 + 0.6 * 1$
$in_{o_1} = 1.105905967$
Input của $o_2$:
$in_{o_2} = w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1$
$in_{o_2} = 0.5 * 0.593269992 + 0.55 * 0.596884378 + 0.6 * 1$
$in_{o_2} = 1.224921404$
Output của $o_1$:
$out_{o_1} = $ $\frac{1}{1 + e^{-in_{o_1}}}$
$out_{o_1} = \frac{1}{1 + e^{-1.105905967}}$
$out_{o_1} = 0.75136507$
Output cuat $o_2$:
$out_{o_2} = $ $\frac{1}{1 + e^{-in_{o_2}}}$
$out_{o_2} = \frac{1}{1 + e^{-1.224921404}}$
$out_{o_2} = 0.772928465$
Tổng lỗi:
$E_{o_1} = \frac{1}{2} (target_{o_1} - out_{o_1})^2$
$E_{o_2} = \frac{1}{2} (0.01 - 0.75136507)^2$
$E_{o_1} = 0.274811083$
$E_{o_2} = \frac{1}{2} (target_{o_1} - out_{o_1})^2$
$E_{o_2} = \frac{1}{2} (0.01 - 0.772928465)^2$
$E_{o_2} = 0.023560026$
$E_{total} = \sum_{i=1}^2 E_{o_i}$
$E_{total} = 0.274811083 + 0.023560026$
$E_{total} = 0.298371109$
2.2 Backward Path
Tính đạo hàm từng phần của Loss Function theo mỗi $w$.
Các $w$ của output layer ($w_5, w_6, w_7, w_8$) có cách tính giống nhau:
- $w_5$:
$\frac{\partial E_{total}}{\partial w_5} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_5}$
Ta biết:
$E_{total} = \sum_{i=1}^2 \frac{1}{2} (target_{o_i} - out_{o_i})^2$
$E_{total} = \frac{1}{2} (target_{o_1} - out_{o_1})^2 + \frac{1}{2} (target_{o_2} - out_{o_2})^2$
Nên:
$\frac{\partial E_{total}}{\partial out_{o_1}}$ $ = 2 * \frac{1}{2} (target_{o_1} - out_{o_1})^{2-1} * (-1) + 0$
$\frac{\partial E_{total}}{\partial out_{o_1}}$ $ = -(target_{o_1} - out_{o_1})$
$\frac{\partial E_{total}}{\partial out_{o_1}}$ $ = -(0.01 - 0.75136507) = 0.74136507$
Tiếp theo, vì:
$out_{o_1} = sigmoid(in_{o_1}) =$ $\frac{1}{1 + e^{-in_{01}}}$
Nên:
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = out_{o_1}(1 - out_{o_1})$
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = 0.75136507(1 - 0.75136507)$
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = 0.186815602$
Và,
$in_{o_1} = w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1$
Nên:
$\frac{\partial in_{o_1}}{\partial w_5}$ $ = out_{h_1}$
$\frac{\partial in_{o_1}}{\partial w_5}$ $ = 0.593269992$
Tổng hợp lại ta được:
$\frac{\partial E_{total}}{\partial w_5} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_5}$$
$\frac{\partial E_{total}}{\partial w_5}$ $ = 0.74136507 * 0.186815602 * 0.593269992$
$\frac{\partial E_{total}}{\partial w_5}$ $ = 0.082167041$
- $w_6$:
$\frac{\partial E_{total}}{\partial w_6} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_6}$
$\frac{\partial E_{total}}{\partial out_{o_1}} = 2 * \frac{1}{2} (target_{o_1} - out_{o_1})^{2-1} * (-1) + 0$$
$\frac{\partial E_{total}}{\partial out_{o_1}}$ $ = -(target_{o_1} - out_{o_1})$
$\frac{\partial E_{total}}{\partial out_{o_1}}$ $ = -(0.01 - 0.75136507) = 0.74136507$
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = out_{o_1}(1 - out_{o_1})$
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = 0.75136507(1 - 0.75136507)$
$\frac{\partial out_{o_1}}{\partial in_{o_1}}$ $ = 0.186815602$
$\frac{\partial in_{o_1}}{\partial w_6} $ $= out_{h_2}$
$\frac{\partial in_{o_1}}{\partial w_6}$ $ = 0.596884378$
Tổng hợp lại ta được:
$\frac{\partial E_{total}}{\partial w_6} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_6}$
$\frac{\partial E_{total}}{\partial w_6}$ $ = 0.74136507 * 0.186815602 * 0.596884378$
$\frac{\partial E_{total}}{\partial w_6} $ $= 0.082667628$
- $w_7$:
$\frac{\partial E_{total}}{\partial w_7} = \frac{\partial E_{total}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial w_7}$
$\frac{\partial E_{total}}{\partial out_{o_2}} = 0 + 2 * \frac{1}{2} (target_{o_2} - out_{o_2})^{2-1} * (-1)$
$\frac{\partial E_{total}}{\partial out_{o_2}}$ $ = -(target_{o_2} - out_{o_2})$
$\frac{\partial E_{total}}{\partial out_{o_2}}$ $ = -(0.99 - 0.772928465) = -0.217071535$
$\frac{\partial out_{o_2}}{\partial in_{o_2}}$ $ = out_{o_2}(1 - out_{o_2})$
$\frac{\partial out_{o_2}}{\partial in_{o_2}} $ $= 0.772928465(1 - 0.772928465)$
$\frac{\partial out_{o_2}}{\partial in_{o_2}} $ $= 0.175510053$
$\frac{\partial in_{o_2}}{\partial w_7}$ $ = out_{h_1}$
$\frac{\partial in_{o_2}}{\partial w_7} $ $= 0.593269992$
Tổng hợp lại ta được:
$\frac{\partial E_{total}}{\partial w_6} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_6}$
$\frac{\partial E_{total}}{\partial w_6} $ $= -0.217071535 * 0.175510053 * 0.593269992$
$\frac{\partial E_{total}}{\partial w_6} $ $= -0.022602541$
- $w_8$:
$\frac{\partial E_{total}}{\partial w_8} = \frac{\partial E_{total}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial w_8}$
$\frac{\partial E_{total}}{\partial out_{o_2}} = 0 + 2 * \frac{1}{2} (target_{o_2} - out_{o_2})^{2-1} * (-1)$
$\frac{\partial E_{total}}{\partial out_{o_2}} $ $= -(target_{o_2} - out_{o_2})$
$\frac{\partial E_{total}}{\partial out_{o_2}} $ $= -(0.99 - 0.772928465) = -0.217071535$
$\frac{\partial out_{o_2}}{\partial in_{o_2}} $ $= out_{o_2}(1 - out_{o_2})$
$\frac{\partial out_{o_2}}{\partial in_{o_2}} $ $= 0.772928465(1 - 0.772928465)$
$\frac{\partial out_{o_2}}{\partial in_{o_2}} $ $= 0.175510053$
$\frac{\partial in_{o_2}}{\partial w_8} $ $= out_{h_2}$
$\frac{\partial in_{o_2}}{\partial w_8} $ $= 0.596884378$
Tổng hợp lại ta được:
$\frac{\partial E_{total}}{\partial w_6} = \frac{\partial E_{total}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial w_6}$
$\frac{\partial E_{total}}{\partial w_6} $ $= -0.217071535 * 0.175510053 * 0.596884378$
$\frac{\partial E_{total}}{\partial w_6} $ $= -0.022740242$
Các $w$ của hidden layer ($w_1, w_2, w_3, w_4$) có cách tính giống nhau:
- $w_1$:
$\frac{\partial E_{total}}{\partial w_1} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_1}$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial out_{h_1}} + \frac{\partial E_{o_2}}{\partial out_{h_1}}$
----------------------------------------------------
$\frac{\partial E_{o_1}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
---------------------------------
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial E_{o_1}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial (\frac{1}{2}(target_{o_1} - out_{o_1})^2)}{\partial out_{o_1}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_1}}})}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_1} - out_{o_1}) * (-1) * out_{o_1}(1 - out_{o_1})$
$\frac{\partial E_{o_1}}{\partial in_{o_1}}$ $ = (0.01 - 0.75136507) * (-1) * 0.75136507(1 - 0.75136507)$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $ $= 0.138498562$
-------------------------
$\frac{\partial in_{o_1}}{\partial out_{h_1}} = \frac{\partial (w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1)}{\partial out_{h_1}}$
$\frac{\partial in_{o_1}}{\partial out_{h_1}}$ $ = w_5$
$\frac{\partial in_{o_1}}{\partial out_{h_1}}$ $ = 0.4$
Gộp lại:
$\frac{\partial E_{o_1}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
$\frac{\partial E_{o_1}}{\partial out_{h_1}}$ $ = 0.138498562 * 0.4$
$\frac{\partial E_{o_1}}{\partial out_{h_1}} $ $= 0.055399425$
----------------------------------------------------
$\frac{\partial E_{o_2}}{\partial out_{h_1}} = \frac{\partial E_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial out_{h_1}}$
---------------------------------
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial E_{o_2}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial (\frac{1}{2}(target_{o_2} - out_{o_2})^2)}{\partial out_{o_2}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_2}}})}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_2} - out_{o_2}) * (-1) * out_{o_2}(1 - out_{o_2})$
$\frac{\partial E_{o_2}}{\partial in_{o_1}}$ $ = (0.99 - 0.772928465) * (-1) * 0.772928465(1 - 0.772928465)$
$\frac{\partial E_{o_2}}{\partial in_{o_1}} $ $= -0.038098237$
-------------------------
$\frac{\partial in_{o_2}}{\partial out_{h_1}} = \frac{\partial (w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1)}{\partial out_{h_1}}$
$\frac{\partial in_{o_2}}{\partial out_{h_1}}$ $ = w_7$
$\frac{\partial in_{o_2}}{\partial out_{h_1}} $ $= 0.5$
Gộp lại:
$\frac{\partial E_{o_2}}{\partial out_{h_1}} = \frac{\partial E_{o_2}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
$\frac{\partial E_{o_2}}{\partial out_{h_1}}$ $ = -0.038098237 * 0.5$
$\frac{\partial E_{o_2}}{\partial out_{h_1}}$ $ = -0.019049118$
---------------------------------
$\frac{\partial E_{total}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial out_{h_1}} + \frac{\partial E_{o_2}}{\partial out_{h_1}}$
$\frac{\partial E_{total}}{\partial out_{h_1}} $$= 0.055399425 + (-0.019049118) = 0,036350307$
----------------------
$\frac{\partial out_{h_1}}{\partial in_{h_1}} = \frac{\partial (\frac{1}{1 + e^{-in_{h_1}}})}{\partial in_{h_1}}$
$\frac{\partial out_{h_1}}{\partial in_{h_1}} $ $= out_{h_1}(1 - out_{h_1})$
$\frac{\partial out_{h_1}}{\partial in_{h_1}}$ $ = 0.59326999(1 - 0.59326999) = 0.241300709$
----------------------
$\frac{\partial in_{h_1}}{\partial w_1} = \frac{\partial (w_1 * i_1 + w_2 * i_2 + b_1 * 1)}{\partial w_1}$
$\frac{\partial in_{h_1}}{\partial w_1}$ $ = i_1$
$\frac{\partial in_{h_1}}{\partial w_1} $ $= 0.05$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial w_1} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_1}$
$\frac{\partial E_{total}}{\partial w_1} $ $= 0.036350306 * 0.241300709 * 0.05$
$\frac{\partial E_{total}}{\partial w_1} $ $= 0.000438568$
- $w_2$:
$\frac{\partial E_{total}}{\partial w_2} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_2}$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial out_{h_1}} + \frac{\partial E_{o_2}}{\partial out_{h_1}}$
----------------------------------------------------
$\frac{\partial E_{o_1}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
---------------------------------
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial E_{o_1}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial (\frac{1}{2}(target_{o_1} - out_{o_1})^2)}{\partial out_{o_1}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_1}}})}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_1} - out_{o_1}) * (-1) * out_{o_1}(1 - out_{o_1})$
$\frac{\partial E_{o_1}}{\partial in_{o_1}}$ $ = (0.01 - 0.75136507) * (-1) * 0.75136507(1 - 0.75136507)$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $ $= 0.138498562$
-------------------------
$\frac{\partial in_{o_1}}{\partial out_{h_1}} = \frac{\partial (w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1)}{\partial out_{h_1}}$
$\frac{\partial in_{o_1}}{\partial out_{h_1}}$ $ = w_5$
$\frac{\partial in_{o_1}}{\partial out_{h_1}}$ $ = 0.4$
Gộp lại:
$\frac{\partial E_{o_1}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
$\frac{\partial E_{o_1}}{\partial out_{h_1}}$ $ = 0.138498562 * 0.4$
$\frac{\partial E_{o_1}}{\partial out_{h_1}} $ $= 0.055399425$
----------------------------------------------------
$\frac{\partial E_{o_2}}{\partial out_{h_1}} = \frac{\partial E_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial out_{h_1}}$
---------------------------------
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial E_{o_2}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial (\frac{1}{2}(target_{o_2} - out_{o_2})^2)}{\partial out_{o_2}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_2}}})}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_2} - out_{o_2}) * (-1) * out_{o_2}(1 - out_{o_2})$
$\frac{\partial E_{o_2}}{\partial in_{o_1}}$ $ = (0.99 - 0.772928465) * (-1) * 0.772928465(1 - 0.772928465)$
$\frac{\partial E_{o_2}}{\partial in_{o_1}} $ $= -0.038098237$
-------------------------
$\frac{\partial in_{o_2}}{\partial out_{h_1}} = \frac{\partial (w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1)}{\partial out_{h_1}}$
$\frac{\partial in_{o_2}}{\partial out_{h_1}}$ $ = w_7$
$\frac{\partial in_{o_2}}{\partial out_{h_1}} $ $= 0.5$
Gộp lại:
$\frac{\partial E_{o_2}}{\partial out_{h_1}} = \frac{\partial E_{o_2}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_1}}$
$\frac{\partial E_{o_2}}{\partial out_{h_1}}$ $ = -0.038098237 * 0.5$
$\frac{\partial E_{o_2}}{\partial out_{h_1}}$ $ = -0.019049118$
---------------------------------
$\frac{\partial E_{total}}{\partial out_{h_1}} = \frac{\partial E_{o_1}}{\partial out_{h_1}} + \frac{\partial E_{o_2}}{\partial out_{h_1}}$
$\frac{\partial E_{total}}{\partial out_{h_1}} $$= 0.055399425 + (-0.019049118) = 0,036350307$
----------------------
$\frac{\partial out_{h_1}}{\partial in_{h_1}} = \frac{\partial (\frac{1}{1 + e^{-in_{h_1}}})}{\partial in_{h_1}}$
$\frac{\partial out_{h_1}}{\partial in_{h_1}} $ $= out_{h_1}(1 - out_{h_1})$
$\frac{\partial out_{h_1}}{\partial in_{h_1}}$ $ = 0.59326999(1 - 0.59326999) = 0.241300709$
----------------------
$\frac{\partial in_{h_1}}{\partial w_2} = \frac{\partial (w_1 * i_1 + w_2 * i_2 + b_1 * 1)}{\partial w_2}$
$\frac{\partial in_{h_1}}{\partial w_2}$ $ = i_2$
$\frac{\partial in_{h_1}}{\partial w_2} $ $= 0.1$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial w_2} = \frac{\partial E_{total}}{\partial out_{h_1}} * \frac{\partial out_{h_1}}{\partial in_{h_1}} * \frac{\partial in_{h_1}}{\partial w_2}$
$\frac{\partial E_{total}}{\partial w_2} $ $= 0.036350306 * 0.241300709 * 0.1$
$\frac{\partial E_{total}}{\partial w_2} $ $= 0.000877135$
- $w_3$:
$\frac{\partial E_{total}}{\partial w_3} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_3}$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial out_{h_2}} + \frac{\partial E_{o_2}}{\partial out_{h_2}}$
----------------------------------------------------
$\frac{\partial E_{o_1}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
---------------------------------
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial E_{o_1}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial (\frac{1}{2}(target_{o_1} - out_{o_1})^2)}{\partial out_{o_1}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_1}}})}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_1} - out_{o_1}) * (-1) * out_{o_1}(1 - out_{o_1})$
$\frac{\partial E_{o_1}}{\partial in_{o_1}}$ $ = (0.01 - 0.75136507) * (-1) * 0.75136507(1 - 0.75136507)$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $ $= 0.138498562$
-------------------------
$\frac{\partial in_{o_1}}{\partial out_{h_2}} = \frac{\partial (w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1)}{\partial out_{h_2}}$
$\frac{\partial in_{o_1}}{\partial out_{h_2}}$ $ = w_6$
$\frac{\partial in_{o_1}}{\partial out_{h_2}}$ $ = 0.45$
Gộp lại:
$\frac{\partial E_{o_1}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
$\frac{\partial E_{o_1}}{\partial out_{h_2}}$ $ = 0.138498562 * 0.45$
$\frac{\partial E_{o_1}}{\partial out_{h_2}} $ $= 0.062324353$
----------------------------------------------------
$\frac{\partial E_{o_2}}{\partial out_{h_2}} = \frac{\partial E_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial out_{h_2}}$
---------------------------------
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial E_{o_2}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial (\frac{1}{2}(target_{o_2} - out_{o_2})^2)}{\partial out_{o_2}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_2}}})}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} $$ = 2 * \frac{1}{2} (target_{o_2} - out_{o_2}) * (-1) * out_{o_2}(1 - out_{o_2})$
$\frac{\partial E_{o_2}}{\partial in_{o_2}}$ $ = (0.99 - 0.772928465) * (-1) * 0.772928465(1 - 0.772928465)$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} $ $= -0.038098237$
-------------------------
$\frac{\partial in_{o_2}}{\partial out_{h_2}} = \frac{\partial (w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1)}{\partial out_{h_2}}$
$\frac{\partial in_{o_2}}{\partial out_{h_2}}$ $ = w_8$
$\frac{\partial in_{o_2}}{\partial out_{h_2}} $ $= 0.55$
Gộp lại:
$\frac{\partial E_{o_2}}{\partial out_{h_2}} = \frac{\partial E_{o_2}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
$\frac{\partial E_{o_2}}{\partial out_{h_2}}$ $ = -0.038098237 * 0.55$
$\frac{\partial E_{o_2}}{\partial out_{h_2}}$ $ = -0.02095403$
---------------------------------
$\frac{\partial E_{total}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial out_{h_2}} + \frac{\partial E_{o_2}}{\partial out_{h_2}}$
$\frac{\partial E_{total}}{\partial out_{h_2}} $$= 0.062324353 + (-0.02095403) = 0.041370323$
----------------------
$\frac{\partial out_{h_2}}{\partial in_{h_2}} = \frac{\partial (\frac{1}{1 + e^{-in_{h_2}}})}{\partial in_{h_2}}$
$\frac{\partial out_{h_2}}{\partial in_{h_2}} $ $= out_{h_2}(1 - out_{h_2})$
$\frac{\partial out_{h_2}}{\partial in_{h_2}}$ $ = 0.596884378(1 - 0.596884378) = 0.240613417$
----------------------
$\frac{\partial in_{h_2}}{\partial w_3} = \frac{\partial (w_3 * i_1 + w_4 * i_2 + b_1 * 1)}{\partial w_3}$
$\frac{\partial in_{h_2}}{\partial w_3}$ $ = i_1$
$\frac{\partial in_{h_2}}{\partial w_3} $ $= 0.05$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial w_3} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_3}$
$\frac{\partial E_{total}}{\partial w_3} $ $= 0.041370323 * 0.240613417 * 0.05$
$\frac{\partial E_{total}}{\partial w_3} $ $= 0.000497713$
- $w_4$:
$\frac{\partial E_{total}}{\partial w_4} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_4}$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial out_{h_2}} + \frac{\partial E_{o_2}}{\partial out_{h_2}}$
----------------------------------------------------
$\frac{\partial E_{o_1}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
---------------------------------
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial E_{o_1}}{\partial out_{o_1}} * \frac{\partial out_{o_1}}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} = \frac{\partial (\frac{1}{2}(target_{o_1} - out_{o_1})^2)}{\partial out_{o_1}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_1}}})}{\partial in_{o_1}}$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $$ = 2 * \frac{1}{2} (target_{o_1} - out_{o_1}) * (-1) * out_{o_1}(1 - out_{o_1})$
$\frac{\partial E_{o_1}}{\partial in_{o_1}}$ $ = (0.01 - 0.75136507) * (-1) * 0.75136507(1 - 0.75136507)$
$\frac{\partial E_{o_1}}{\partial in_{o_1}} $ $= 0.138498562$
-------------------------
$\frac{\partial in_{o_1}}{\partial out_{h_2}} = \frac{\partial (w_5 * out_{h_1} + w_6 * out_{h_2} + b_2 * 1)}{\partial out_{h_2}}$
$\frac{\partial in_{o_1}}{\partial out_{h_2}}$ $ = w_6$
$\frac{\partial in_{o_1}}{\partial out_{h_2}}$ $ = 0.45$
Gộp lại:
$\frac{\partial E_{o_1}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
$\frac{\partial E_{o_1}}{\partial out_{h_2}}$ $ = 0.138498562 * 0.45$
$\frac{\partial E_{o_1}}{\partial out_{h_2}} $ $= 0.062324353$
----------------------------------------------------
$\frac{\partial E_{o_2}}{\partial out_{h_2}} = \frac{\partial E_{o_2}}{\partial in_{o_2}} * \frac{\partial in_{o_2}}{\partial out_{h_2}}$
---------------------------------
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial E_{o_2}}{\partial out_{o_2}} * \frac{\partial out_{o_2}}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} = \frac{\partial (\frac{1}{2}(target_{o_2} - out_{o_2})^2)}{\partial out_{o_2}} * \frac{\partial (\frac{1}{1 + e^{-in_{o_2}}})}{\partial in_{o_2}}$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} $$ = 2 * \frac{1}{2} (target_{o_2} - out_{o_2}) * (-1) * out_{o_2}(1 - out_{o_2})$
$\frac{\partial E_{o_2}}{\partial in_{o_2}}$ $ = (0.99 - 0.772928465) * (-1) * 0.772928465(1 - 0.772928465)$
$\frac{\partial E_{o_2}}{\partial in_{o_2}} $ $= -0.038098237$
-------------------------
$\frac{\partial in_{o_2}}{\partial out_{h_2}} = \frac{\partial (w_7 * out_{h_1} + w_8 * out_{h_2} + b_2 * 1)}{\partial out_{h_2}}$
$\frac{\partial in_{o_2}}{\partial out_{h_2}}$ $ = w_8$
$\frac{\partial in_{o_2}}{\partial out_{h_2}} $ $= 0.55$
Gộp lại:
$\frac{\partial E_{o_2}}{\partial out_{h_2}} = \frac{\partial E_{o_2}}{\partial in_{o_1}} * \frac{\partial in_{o_1}}{\partial out_{h_2}}$
$\frac{\partial E_{o_2}}{\partial out_{h_2}}$ $ = -0.038098237 * 0.55$
$\frac{\partial E_{o_2}}{\partial out_{h_2}}$ $ = -0.02095403$
---------------------------------
$\frac{\partial E_{total}}{\partial out_{h_2}} = \frac{\partial E_{o_1}}{\partial out_{h_2}} + \frac{\partial E_{o_2}}{\partial out_{h_2}}$
$\frac{\partial E_{total}}{\partial out_{h_2}} $$= 0.062324353 + (-0.02095403) = 0.041370323$
----------------------
$\frac{\partial out_{h_2}}{\partial in_{h_2}} = \frac{\partial (\frac{1}{1 + e^{-in_{h_2}}})}{\partial in_{h_2}}$
$\frac{\partial out_{h_2}}{\partial in_{h_2}} $ $= out_{h_2}(1 - out_{h_2})$
$\frac{\partial out_{h_2}}{\partial in_{h_2}}$ $ = 0.596884378(1 - 0.596884378) = 0.240613417$
----------------------
$\frac{\partial in_{h_2}}{\partial w_4} = \frac{\partial (w_3 * i_1 + w_4 * i_2 + b_1 * 1)}{\partial w_3}$
$\frac{\partial in_{h_2}}{\partial w_4}$ $ = i_2$
$\frac{\partial in_{h_2}}{\partial w_4} $ $= 0.1$
--------------------------------------------------------------
$\frac{\partial E_{total}}{\partial w_4} = \frac{\partial E_{total}}{\partial out_{h_2}} * \frac{\partial out_{h_2}}{\partial in_{h_2}} * \frac{\partial in_{h_2}}{\partial w_4}$
$\frac{\partial E_{total}}{\partial w_4} $ $= 0.041370323 * 0.240613417 * 0.1$
$\frac{\partial E_{total}}{\partial w_4} $ $= 0.000995425$
Đến đây ta đã tính xong các đạo hàm từng phần theo các $w$. Áp dụng SGD để cập nhật các $w$ ta được (chọn $\eta = 0.9$):
$w_5^+ = w_5 - \eta * $$\frac{\partial E_{total}}{\partial w_5}$
$w_5^+ = 0.4 - 0.9 * 0.082167041$
$w_5^+ = 0.326049663$
-------------------------
$w_6^+ = w_6 - \eta * $$\frac{\partial E_{total}}{\partial w_6}$
$w_6^+ = 0.45 - 0.9 * 0.082667628$
$w_6^+ = 0.375599135$
-------------------------
$w_7^+ = w_7 - \eta * $$\frac{\partial E_{total}}{\partial w_7}$
$w_7^+ = 0.5 - 0.9 * (-0.022602541)$
$w_7^+ = 0.520342287$
-------------------------
$w_8^+ = w_8 - \eta * $$\frac{\partial E_{total}}{\partial w_8}$
$w_8^+ = 0.55 - 0.9 * (-0.022740242)$
$w_8^+ = 0.570466218$
-------------------------
$w_1^+ = w_1 - \eta * $$\frac{\partial E_{total}}{\partial w_1}$
$w_1^+ = 0.15 - 0.9 * 0.000438568$
$w_1^+ = 0.149605289$
-------------------------
$w_2^+ = w_2 - \eta * $$\frac{\partial E_{total}}{\partial w_2}$
$w_2^+ = 0.2 - 0.9 * 0.0080877135$
$w_2^+ = 0.192721058$
-------------------------
$w_3^+ = w_3 - \eta * $$\frac{\partial E_{total}}{\partial w_3}$
$w_3^+ = 0.25 - 0.9 * 0.000497713$
$w_3^+ = 0.249552058$
-------------------------
$w_4^+ = w_4 - \eta * $$\frac{\partial E_{total}}{\partial w_4}$
$w_4^+ = 0.3 - 0.9 * 0.000995425$
$w_4^+ = 0.299104118$
-------------------------
Phù, như vậy là chúng ta đã cập nhật xong giá trị mới cho các trọng số $w$. Đây là những phép toán xảy ra trong mỗi lần cập nhật khi training model. Hi vọng, thông qua ví dụ trong bài này, các bạn đã có thể hiểu rõ hơn bản chất của mạng NN. Hẹn gặp lại các bạn trong các bài tiếp theo!
3. Tham khảo